A 22 B 24 (delw)/(delx) = x/sqrt(x^2 y^2 z^2) (delw)/(dely) = y/sqrt(x^2 y^2 z^2) (delw)/(delz) = z/sqrt(x^2 y^2 z^2) Since you're dealing with a multivariable function, you must treat x, y, and z as independent variables and calculate the partial derivative of w, your dependent variable, with respect to x, y, and z When you differentiate with respect to x, you treat y and z asLagrange Multipliers Minimum of f(x, y, z) = x^2 y^2 z^2 subject to x y z 9 = 0

How To Do Implicit Differentiation 7 Steps With Pictures
F x 2 y 2 z 2 z 2-2xy 0
F x 2 y 2 z 2 z 2-2xy 0-X^2y^2z^2xyyzzx=0 multiplying the RHS and LHS by 2 we get , 2 x^2y^2z^2xyyzzx =0 or, (xy)^2 (yz)^2 (zx)^2=0 since in LHS there are only squared terms,ie they cannot be negative and since they are all equal to zero therefore each term must also equal to zero ie (xy)^2=0 , (yz)^2=0 , (zx)^2=0Click here👆to get an answer to your question ️ If u = f(r) , where r^2 = x^2 y^2 then ( ∂^2u∂x^2 ∂^2u∂y^2 ) =




If 2x 2 2y 2 2x 2y 1 0 Then What Is The Value Of X Y Quora
To eliminate the function f(x^2 xy) you can take u = x^2 xy This gives z = f( u(x,y) ) The derivatives respect to x and y are z_x = f'(u)u_x = f'(u)(2x y) z_y = f'(u)u_y = f'(u)x Then f'(u) = z_x/(2xy) = z_y/x ,The PDE is z_x/(2xy) z_y/x =0 CHo ba số x,y,z khác nhau và khác 0 thỏa mãn \(\dfrac{1}{x}\dfrac{1}{y}\dfrac{1}{z}=0\) C/m \(\dfrac{1}{x^22yz}\dfrac{1}{y^22xz}\dfrac{1}{z^22xy}=0\)Simple and best practice solution for x^2y^2z^22xy2xz2yx=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework
⇒ (x y) 2 z 2 ∴ (a 2 b 2) = (a b) (a b) ⇒ (x y z) (x y z) As we know, (x y z) = 0 ∴ x 2 y 2 z 2 2xy = 0 × (x y z) = 0 Join The Discussion Comment * Related Questions on Algebra If a * b = 2a 3b ab, then 3 * 5 5 * 3 is equal to?F = bxy2,bx2y,(x2 y2)z2 and S is the closed surface bounding the region D consisting of the solid cylinder x2 y2 6 a2 and 0 6 z 6 b Solution This is a problem for which the divergence theorem is ideally suited Calculating the divergence of → F, we get → ∇→ F = h∂x,∂y,∂zi bxy 2,bx2y,(x2 y2)z2 = (x2 y )(b2z) Applying the divergence theorem we get ZZ S 0 The case p = 2 is dealt with by explcit counting So assume p > 2 Let m be the number of solutions F p × acts on the set of solution by coordinatewise multiplication, where we have ( c x, c y, c z) = ( x, y, z) iff c = 1 or x = y = z = 0, that is all orbits except that of the trivial solution have length p − 1
Cm x^2 y^22xy xy 1 >0 HOC24 Lớp học Lớp học Tất cả Lớp 12 Lớp 11 Lớp 10 Lớp 9 Lớp 8 Lớp 7 Lớp 6 Lớp 5 Lớp 4 Lớp 3 Lớp 2 Lớp 1 Hỏi đáp ĐềA) ϕ(xyz, y z) = 0 B) ϕ(y z, y x2 y2 z2) = 0 C) ϕ(y 2, z 2) = 0 D) None of these Correct Answer B) ϕ(y z, y x2 y2 z2) = 0 Part of solved Aptitude questions and answers >> Aptitude Login to BookmarkTìm x, y, z biết 2x^22y^2z^22xy2xz2yz10x6y34=0 Tìm x;



1




How To Do Implicit Differentiation 7 Steps With Pictures
F X 2 Y 2 Z 2 Z 2 2xy 0 c class mercedes benz 21 models c class mercedes coupe c clamps lowes c class coupe amg c class coupe c class mercedes benz sedan c clamp storage rack c clamps for woodworking c class mercedes 10 interior c class c300 coupe c class c300 mercedes ( x^2y^2z^2)^2 4x^2y^2 ( (x^2 y^2 z^2 2xy ) ( x^2 y^2 z^2 2xy ) ( x^2 2xy y^2 z^2 ) ( x^2 2xy y^2 z^2 ) ( ( x y)^2 z^2 ) ( ( x y)^2 z^2 ) ( (x y) z ) ( (x y ) z ) ( (x y) z) ( ( x y) z ) ( x y z ) ( x y z) ( x y z ) ( x y z )Assume the variables are restricted to values that prevent division by 0 (x^2y^2)/(x^22xyy^2) divided by (3x3y)/(7x21) Could someone please show me how to do this so I can do algebra can some one please help figure this problem out Determine whether each expression is a polynomialIf it is a polynomial, state the degree of the




Evaluate Each Of The Following Expressions For X 2 Y 1 Z 3 I X Y Y Z Z X Ii X 2 Y 2 Z 2 X Y Y Z Z X



Stewartcalculus Com Data Essential calculus 2e Upfiles Instructor Ess Ax 1102 Pdf
Differentiating equation (1) partially wrt x & y, we get Eliminating a and b from equations (1), (2) and (3), we get a partial differential equation of the first order of the form f (x,y,z, p, q) = 0 Example 1 Eliminate the arbitrary constants a & b from z = ax by ab1 8 dt= udu changing the bounds, we get = 1 2 Z 5 1 1 4 (t 1) p t 1 8 dt = 1 64 Z 5 1 t3=2 t1=2 dt 1 64 2 5 t5=2 2 3 t3=2 5 1 = 5 48 p 5 1 240 11 Evaluate RR S x 2z2 dS, where Sis the part of the cone z2 = x2 y between the planes z= 1 and z= 3 The widest point of Sis at the intersection of the cone and the plane z= 3, where x2 y2 = 32 = 9;The directional derivative of the surface, f = (x 2 y 2 z 2) at the point P 2, 2, 1 T along the vector a = 1, 1, 0 T is given by



Www Tau Ac Il Levant Ode Solution 6 Pdf




15 2xy Y 2 Dx 2xy X 2 2x 2y 2 2xy 3 Dy 0 Homeworklib
Add the two equivalent fractions which now have a common denominator Combine the numerators together, put the sum or difference over the common denominator then reduce to lowest terms if possible (x2y2) • 4 z2 4x2 4y2 z2 ———————————————— = —————————————— 4 4Substitute t= 4u2 1;u2 = 1 4 (t 1);F'(1,1,1)=2偏x f'(1,1,1)=2偏y f'(1,1,1)=2偏z cosa=3/根号50 cosb=4/根号50 cosc=5/根号50 f(x,y,z)=x^2y^2z^2在点(1,1,1)处,沿向量(3,4,5)的方向导数=f'(1,1,1)偏x*cosaf'(1,1,1)偏y*cosbf'(1,1,1)偏z*cosc 代入即可



Http Www Disconzi Net Teaching Mat2300 Fall 16 Extras Practice Test 2 Solutions Pdf




Partial Differential Equations
$=\dfrac{yz}{(xy)(xz)}\dfrac{zx}{(yz)(yx)}\dfrac{xy}{(zx)(zy)}$ $=\dfrac{xy(xy)yz(yz)zx(zx)}{(xy)(yz)(zx)}$ Giải thích giùm mình chỗ nàyAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsF2(x, y, z) = 2x^2 y^2 − 4z = 0 f3(x,y,z) = 3x^2 −4yz^2 = 0 This system can be concisely represented as F(x) = 0, where F(x) = (f1, f2, f3)T , x=(x,y,z)T and 0 = (0,0,0)T (transpose written because these should be column vectors)




Math 6c Chapter 12 Quiz



Multiply X2 4y2 Z2 2xy Xz 2yz By Z X 2y Studyrankersonline
X^2+y^2-z^2+2xy/x^2-y^2+z^2-2xz =(xy)^2z^2 / (xz)^2y^2 =xyz /xyzآلة حاسبة للجبر حلول لمسائل جبريّة خطوة بخطوةZ biết \(2x^22y^2z^22xy2xz2yz10x6y34=0\) Theo dõi Vi phạm YOMEDIA Toán 8 Bài 8 Trắc nghiệm Toán 8 Bài 8 Giải bài tập Toán 8 Bài 8 Trả lời (2) \(2x^22y^2z^22xy2xz2yz10x6y34=0\)



Www Ualberta Ca Rjia Math214 Hwks Sol8 Pdf
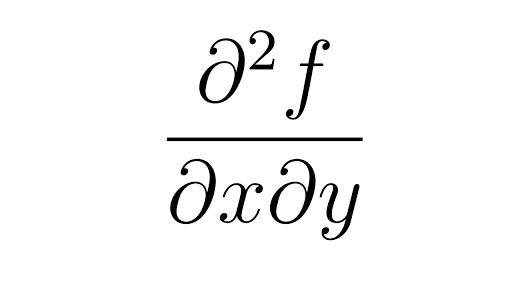



Second Partial Derivatives Article Khan Academy
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more If x y z = 0, then \(\frac{x^2}{2x^2yz}\frac{y^2}{2y^2zx}\frac{z^2}{2z^2xy}\) = (a) 4 (b) 2 (c) 3 (d) 1 Login RememberZ 0 −2 Z √ 4−x2 0 x2 y2 dy dx Z √ 2 0 Z √ 4−x2 x x2 y2 dy dx Solution2 2 x x y = 42 2 y y = x 2 I = Z π π/4 Z 2 0 r2 rdr dθ I = 3π 4 r4 4 2 0 We conclude I = 3π C Triple integral in Cartesian coordinates (Sect 155) Example Find the volume of the region in the first octant below the plane 2x y − 2z = 2 and x 6



Http Www Math Ntu Edu Tw Cheng Teaching Calculus Ch15 Pdf




Graphs Of Surfaces Z F X Y Contour Curves Continuity And Limits
Y Simplify —— x 2 Equation at the end of step 1 y (((((x 2)(y 2))(z 2))(2x•——))y 2)z 2)2xz x 2 Step 2 Rewriting the whole as an Equivalent Fraction 21 Subtracting a fraction from a whole Rewrite the whole as a fraction using x as the denominatorExtended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, musicAnswer to Let f(x,y,z)=x^2y^2z^2 and let S be the level surface defined by f(x,y,z) = 4 (a) Find an equation for the plane tangent to S




Lagrange Multipliers Minimize F X Y X 2 Y 2 Subject To X 2y 5 0 Youtube




Unit 2
Find an answer to your question factorize x^2y^2z^22xy samir1747 samir1747 Math Secondary School answered Factorize x^2y^2z^22xy 1 See answer samir1747 is waiting for your help Add your answer and earn points{eq}F(x,y,z) = (xy 2xz)i (x^2 y^2)j (xy z^2)k {/eq} S is the surface of the solid bounded by the cylinder {eq}x^2y^2=4 {/eq} and the planes z =y 2 and z = 0若有一扇形的周长为60 cm,那么扇形的最大面积为A500 cm2B60 cm2C225 cm2D30 cm2




2 Partial Differentiation



Find The Minimum Value Of X 2 Y 2 Z 2 Subject To The Conditions Xy Yz Zx 3a 2 Sarthaks Econnect Largest Online Education Community
x3y4z = 0 First we rearrange the equation of the surface into the form f(x,y,z)=0 x^22z^2 = y^2 x^2 y^2 2z^2 = 0 And so we have our function f(x,y,z) = x^2 y^2 2z^2 In order to find the normal at any particular point in vector space we use the Del, or gradient operator grad f(x,y,z) = (partial f)/(partial x) hat(i) (partial f)/(partial y) hat(j) (partial f)/(partial zView pde paul21pdf from MATH 121 at Jomo Kenyatta University of Agriculture and Technology, Nairobi 2 Eliminate the arbitrary function f from the equations ans (y − z)p (z − x)q = x −We have x^2y^2=36z^2 and xy=10z, which gives (10z)^22xy=36z^2 or xy=3210zz^2 and xyz=32z10z^2z^3 Also, (xy)^2\geq4xy, which gives 3z^2z28\leq0 or 2\leq z\leq\frac{14}{3} We have x 2 y 2 = 3 6 − z 2 and x y = 1 0 − z , which gives ( 1 0 − z ) 2 − 2 x y = 3 6 − z 2 or x y = 3 2 − 1 0 z z 2 and x y z = 3 2 z − 1 0 z 2 z 3



Answers To The Review Problems For The First Exam 251 05 10 In Spring 06




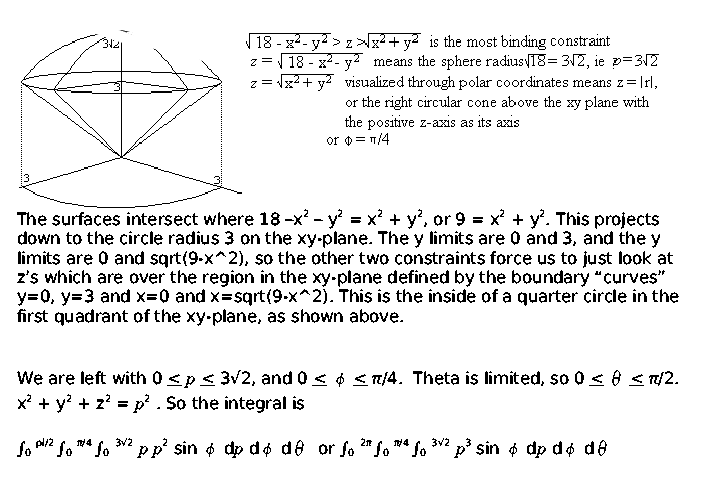
Answered Use Spherical Coordinates To Find The Bartleby
关注 展开全部 2x^2y^2z^22xy1=0化简 (xy)^2x^2z^21=0 用u= (xy),v=x则x,y,z的坐标原点在u,v,z坐标系中坐标是(00,0,0)也是原点。 在u,v,z坐标系中 z^2=u^2v^21是一个典型的图,在高数书上有,其性质是在xy平面上,是一个双V型,沿着z轴,看是一个不断变大的圆Click here👆to get an answer to your question ️ multiply x^2 4y^2 z^2 2xy xz 2yz by ( z x 2y )If F = ( x 2, y 2, z 2), S = { x 2 y 2 z 2 = 1, z ≥ 0 }, evaluate ∬ S F d S I'm having trouble computing this In spherical coordinates we get which is really hard to evaluate But we know that the normal vector to the sphere is r = ( x, y, z), hence, Can we say that the first summand evaluates to zero since S is symmetrical with respect to



Http People Math Umass Edu Bill M233 Study Guide2 S13 Pdf



How To Eliminate The Arbitrary Function And Hence Obtain The Partial Differential Equation Z X Y F X 2 Y 2 Quora




Multiply X 2 4y 2 Z 2 2xy Xz 2yz By Z X 2y



Http Www Math Sci Hokudai Ac Jp S Settepanella Teachingfile Calculus Calculus2 Pagine Lineintex Pdf



Search Q Elimination Of Arbitrary Functions Solved Problems Tbm Isch




X Y Z Belong To R X Y Z 4 X 2 Y 2 Z 2 6 Find Maximum Possible Value Of Z Mathematics Topperlearning Com 2j1z7sww




F X Y Z X 2y Y 2z Xz 2 Partial Differential Chegg Com




How To Do Implicit Differentiation 7 Steps With Pictures



Http Www Math Tamu Edu Glahodny Math251 Section 12 8 Pdf



Http Www Math Mcgill Ca Labute Courses 265a 01 Ps3 Pdf



Http Www Math Ntu Edu Tw Cheng Teaching Calculus Ch15 Pdf



Faculty Math Illinois Edu Franklan Math241 168 Stokesthm Pdf




1 9 3 We Would Like To Make The Length 6 The Only Vectors In The Same Direction As V Are Those Pdf Free Download



Math Mit Edu Jorloff 18 04 Notes Topic5 Pdf




For F X Y X 2 Y 2 2xy Sketch F A For X 0 Mathematics Stack Exchange




Finding An Equation Of A Tangent Plane In Exercises Chegg Com




Factorise X 2 Y 2 Z 2 2xy 2xz 2yz Brainly In



Solved Find The Integral Surface Of The Partial Differential Equation 2xy 1 P Z 2x3 Q 2 X Yz Through Curves X 1 And Y 0 Course Hero



Www Whitman Edu Mathematics Multivariable Multivariable 14 Partial Differentiation Pdf




Vector Analysis By Alimkanwalimtinaa Issuu
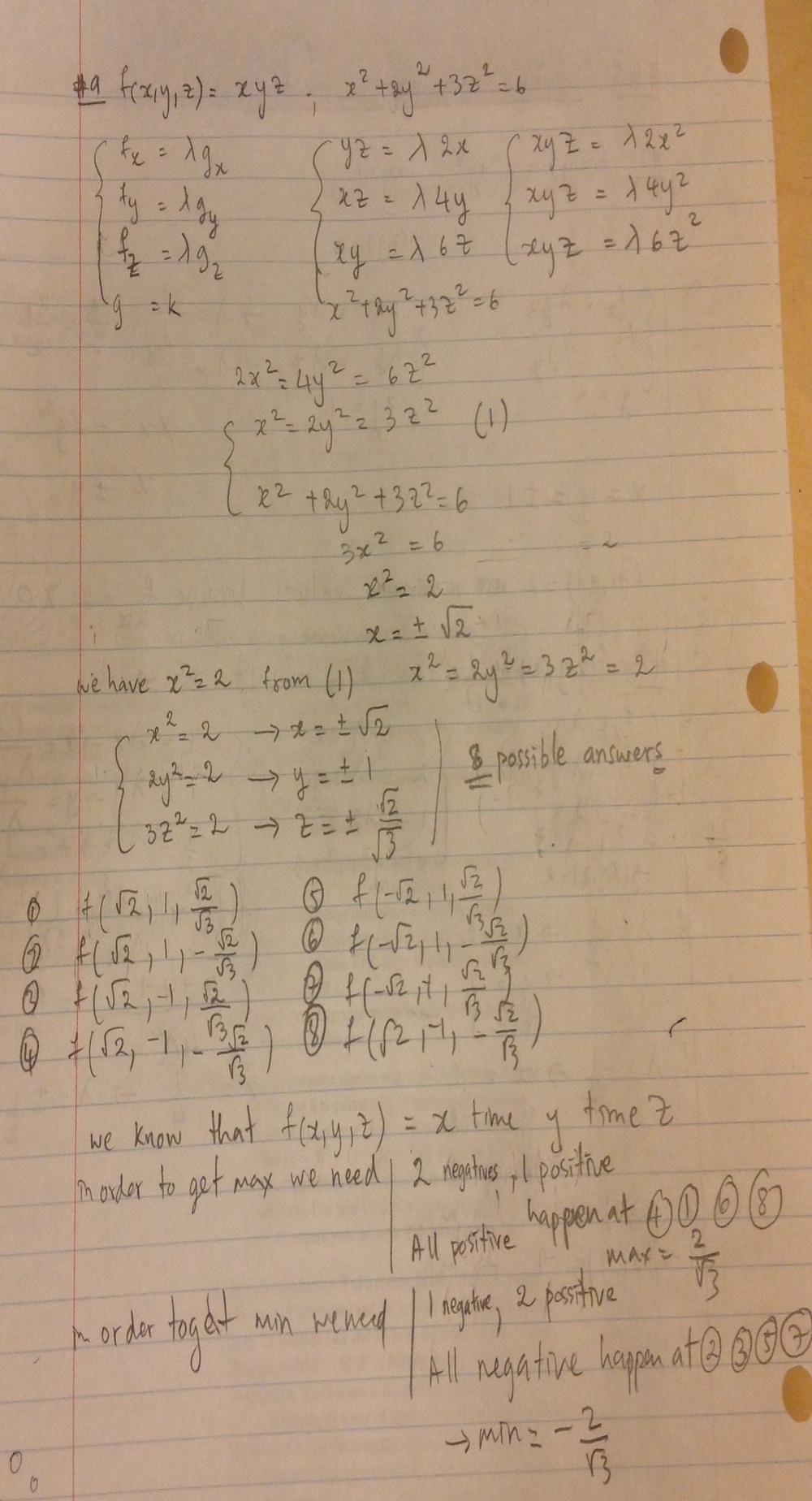



Use Lagrange Multipliers To Find The Maximum And Minimum Values Of The Function Subject To The Given Constraint F X Y Z Xyz X 2 2y 2 3z 2 6 Homework Help And Answers Slader



Surface Area




For The Differential Equation X 2 Y 2 Dx 2xy Dy 0 Which Of The Following Are True Youtube
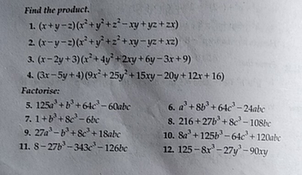



Find The Product 1 X Y Z X2 Y2 Z2 Xy Yz Zx 4 Gr Scholr




If U Log X 2 Y 2 Z 2 Then Prove That X 2 Y 2 Z 2 D 2u Dx 2 D 2u Dy 2 D 2u Dz 2 1




1a If Z F X Y With X E T Y T 2 3t 2 Upsidedown Delta F 2xy 2 Y 2x 2y X Find Z T At T 0 B Parametrize Surface Y 2 2 Z 3 2 4 Please Answer Asap For Thumbs Up Thanks Homeworklib



Orion Math Iastate Edu Butler Calculus Exams Butler 265f11pt2asolns Pdf



Q Tbn And9gcq69xqaiwgxy95 44f5sqsm2pnlgxvor Roue6xadfczqpkv4qx Usqp Cau



Surface Area




Z 2i



Www Amherst Edu System Files Solution 25practice 25test 253 0 Pdf
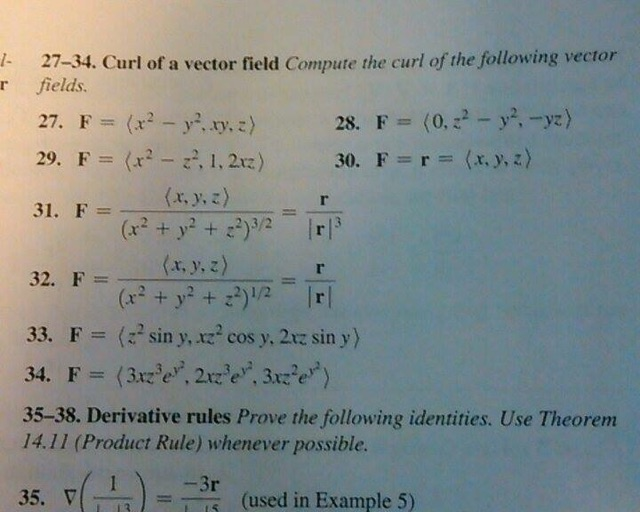



Curl Of A Vector Field Compute The Curl Of The Chegg Com



What Is The Form A Pde By Eliminating The Arbitrary Function Phi From Phi X 2 Y 2 Z 2 Z 2 2xy 0 Can Someone Solve It Quora




Satyabama Niversity Questions In Vector



14 7 Maximum And Minimum Values Mathematics Libretexts



2




Assignment On Numerical Methods




Level Set Examples Math Insight



Math Okstate Edu People Binegar 4013 U98 4013 S03 Pdf




Extremes Of F X Y Z X 1 2y 2 Z 1 2 With X 2 Y 2 Z 2 Leq 1 Mathematics Stack Exchange




X Y Z 0 Show That X3 Y3 Z3 3xyz Novocom Top



Q Tbn And9gcq8jeckpyefv6nxxng4iwjfl7hsluh Liz05p1lqjy Usqp Cau



Www3 Nd Edu Taylor Math550 Images Currentexamsolutions Exam4f16 Pdf




Ex 9 5 15 Class 12 Find Solution 2xy Y 2 2x 2 Dy Dx 0 When




If 2x 2 2y 2 2x 2y 1 0 Then What Is The Value Of X Y Quora



Www Ualberta Ca Rjia Math215 Hwks Sol8 Pdf




Find The General Solution Of I X 2 Y 2 P 2xy Q Chegg Com




5 Find F X F Y And F 2 Where Fx Y Z 15 10 X2 Y2 Gauthmath




Exact Equations Example 3 Video Khan Academy



Www Mathcs Duq Edu Haensch 304materials Chapter2 Pdf




2xy Z2 X2 Y2 See How To Solve It At Qanda



Www Ualberta Ca Csproat Homework Math 215 Solution 7 Pdf




Consider Minimizing And Or Maximizing A Function Z F X Y Subject To A Constraint G X Y C Y Z X Z F X Y Parametrize The Curve Defined By G X Y Ppt Download




Maxima And Minima




Prove That U X 2 Y 2 2xy 2x 3y Is Harmonic And Find Harmonic Conjugate V Edurev Iit Jam Question




5 Charpit S Method Pdf Nonlinear System Differential Equations




Solutions To Implicit Differentiation Problems



Link Springer Com Content Pdf m 3a978 1 349 3 2f1 Pdf




The Image Of The Positive Octant Of The Unit Sphere A X 2 Y 2 Z Download Scientific Diagram
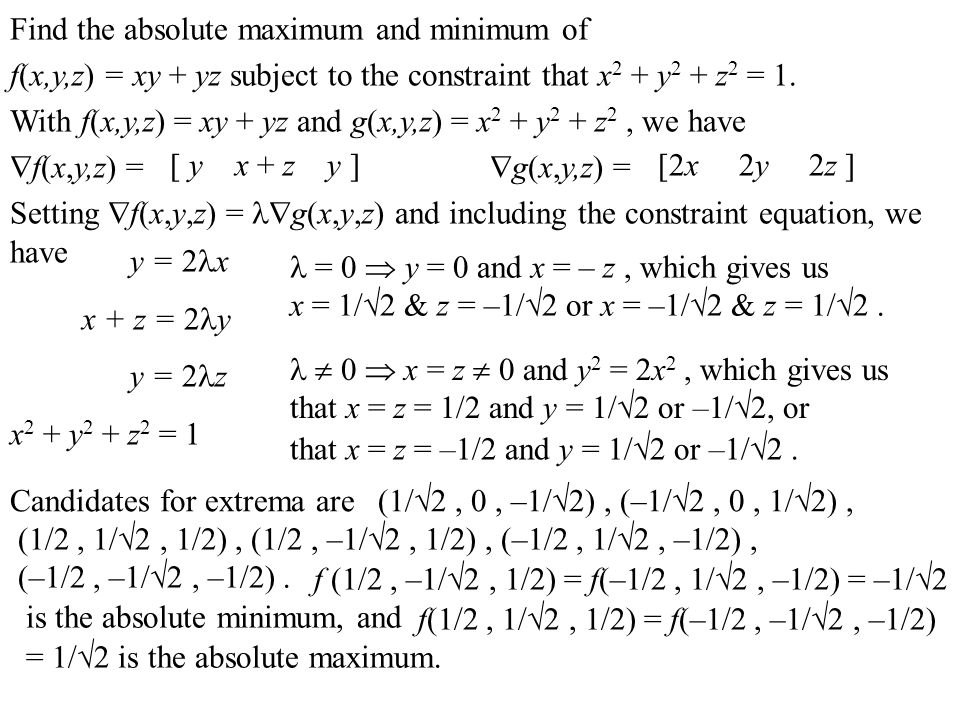



Consider Minimizing And Or Maximizing A Function Z F X Y Subject To A Constraint G X Y C Y Z X Z F X Y Parametrize The Curve Defined By G X Y Ppt Download




Given F X Y Z X 2 Y X Z 4 Find F 3 5 2 Chegg Com




Vector Analysis By Alimkanwalimtinaa Issuu



2



Http Www Maths Gla Ac Uk Cc 2a 2a Notes Chap1notes Sol Pdf




Graphs Of Surfaces Z F X Y Contour Curves Continuity And Limits



Www3 Nd Edu Taylor Math550 Images Worksheets Solutions06 Pdf



If X 2 Y 2 Z 2 2 X Y Z 3 What Is The Value Of 2x 3y 4z Quora




Answered Q1 Find The Derivative Of Bartleby




Partial Differential Equations



Http Www Math Sci Hokudai Ac Jp S Settepanella Teachingfile Calculus Calculus2 Pagine Lineintex Pdf




If X Y Z 0 Then X 2 Yz Y 2 Zx Z 2 Xy Equals A 1 B 2 C 3 Brainly In




Answers To The Review Problems For The First Exam 251 05 10 In Spring 06



If X 2 Y 2 Z 2 2xyz 1 Then Prove That Dx 1 X 2 Dy 1 Y 2 Dz 1 Z 2 0 Sarthaks Econnect Largest Online Education Community




Factorising Cyclic Expression X 2 Y Z Y 2 Z X Z 2 X Y Youtube




1 9 3 We Would Like To Make The Length 6 The Only Vectors In The Same Direction As V Are Those Pdf Free Download




Dy Dx X 2 Y 2 Novocom Top



Surfaces




Use Lagrange Multipliers To Find The Maximum And Minimum Values Of The Function Subject To The Given Constraint F X Y Z Xyz X 2 2y 2 3z 2 6 Homework Help And Answers Slader




Practice Problems 10 And 11




If U Log X 2 Y 2 Z 2 Verify 2u X Y 2u X Y
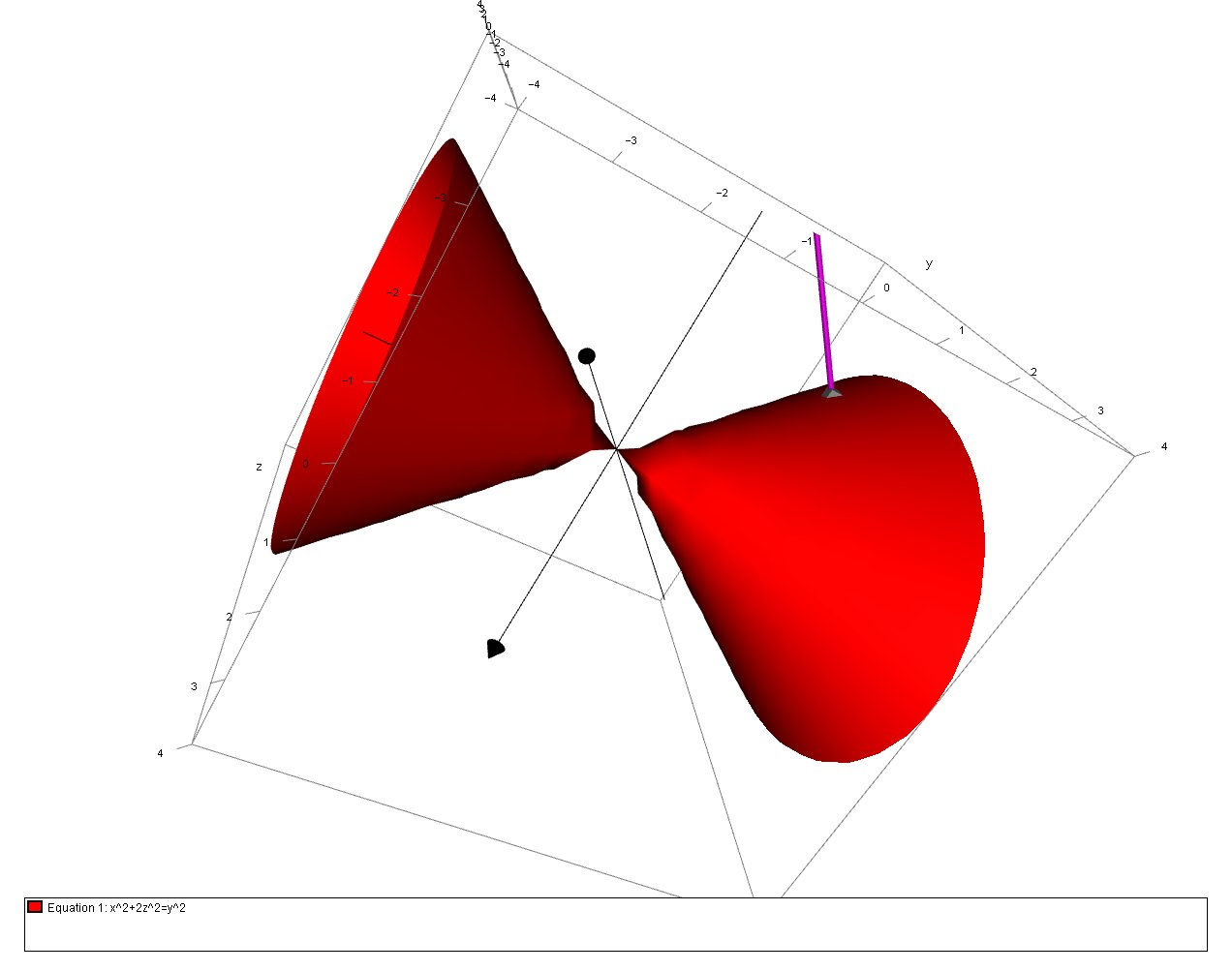



How Do You Find The Equations For The Tangent Plane To The Surface X 2 2z 2 Y 2 Through 1 3 2 Socratic



3d Surface Plotter Academo Org Free Interactive Education



Http Maths Dur Ac Uk Users Daniel Evans Mes Messolutionsupdated Pdf




Ex 9 5 15 Class 12 Find Solution 2xy Y 2 2x 2 Dy Dx 0 When



0 件のコメント:
コメントを投稿