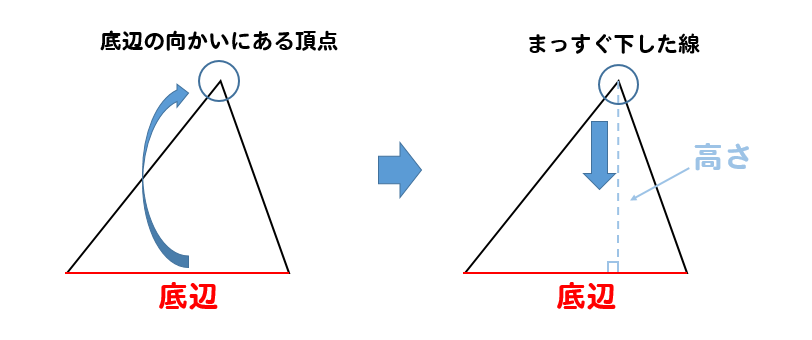
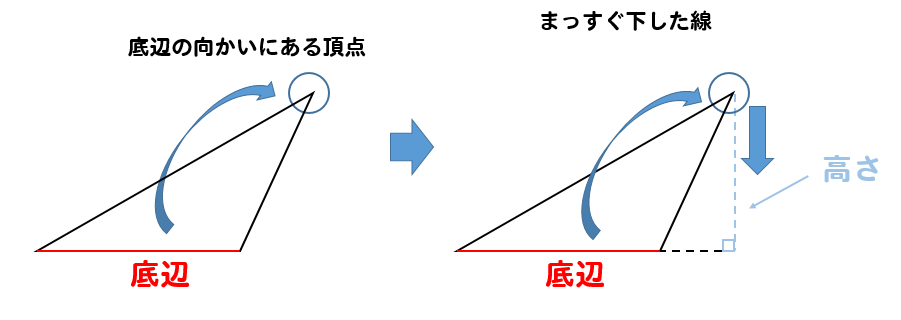
ります。高さが2倍,3倍になると面積も 2倍,3倍となります 三角形の面積は,底辺×高さ÷2で求めることができる。 ちょう点Aが変わっても直線アとイは平行なので高さは変 わらない。 底辺はそのままなので,底辺の長さは変わらない。 三角形の面積=底辺×高さ÷2 です。 ここで、比例の式を思い出してください。 y=ax (aは比例定数) y=a×x です。 比例はxが2倍、3倍になると、yも2倍、3倍になるということです。 三角形の面積の公式を比例の式とよく比べて見てみましょう。「高さの等しい三角形や四角形の面積比=底辺の長さや(上底+下底)の長さの比」 となることを利用して解く問題です。 三角形abeの面積:台形aecdの面積 =底辺be×高さab÷2:(上底ad下底ec)×高さab÷2 =底辺be:(上底ad下底ec)
三角形の面積公式 小学生はどうやって解く 問題を使って解説 数スタ
底辺×高さ÷2 何年生
底辺×高さ÷2 何年生-底辺 × 高さ÷ 2 =三角形の面積 の中を計算して求めなさい。 例示して,助走問題を解かせる。 ⑩ 念のためもう一問出します。 底辺が10cmで,面積がcm2の三角形があります。高さは何cmでしょう面積 正方形 = 一辺 × 一辺 長方形 = 縦 × 横 平行四辺形 = 底辺 × 高さ 三角形 = 底辺 × 高さ ÷ 2 台形 = (上底 下底)× 高さ ÷ 2 ひし形 = 対角線 × 対角線 ÷ 2 円 = 半径 × 半径 × 円周率 弧 = 半径 × 半径 × 円周率 × 弧の角度 ÷ 360




至急 この下の写真の問題の がわかりません Clear
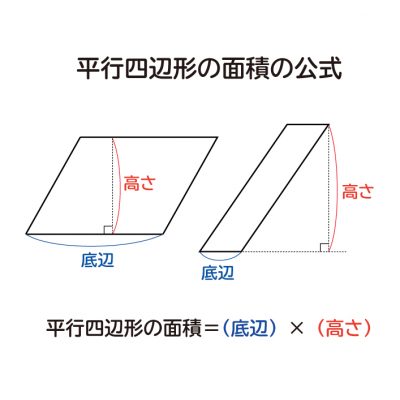
① 「例えば、1こだったら、2こだったら・・・と文字に数を入れて 考えると・・・。」 考え方② 言葉の式や面積の求め方を考えると・・・ (底辺)×(高さ)=平行四辺形の面積 考え方③ の値が3の =y のxに3を代入すると・・・ 場 面 おり紙が12枚 まいこの平行四辺形の面積は「底辺×高さ」=「(上底+下底)×高さ」 で求めることができます。 そのため、 台形の面積は平行四辺形の面積の半分なので「(上底+下底)×高さ÷2」 で求めることができます。 ぴよ校長 台形を2つくっ付けて、平行四辺形を作ることができたね! まとめ ・ 同じ形の台形を2つ使って、平行四辺形を作る ことができます。 ・ 台形の三角形の面積を求める公式 三角形の面積=底辺×高さ÷2 (ていへん かける たかさ わる2) 公式の理解ができたら、公式を覚える練習もさせましょう。 聞いてあげて下さい。 面積の表し方は、4年生の時に、マス目がいくつあるかを考えさせ、後に1㎠を教え
では、次の文の共通する漢字の形と音は、何でしょう? 1 高学年になると、責任が大きくなる。 2 三角形の面積を求める公式は、底辺×高さ÷2。 3 5年生のときよりも成績が上がった。 同じ部分で同じ音ひし形の面積の公式 ひし形の面積は 2 2 つの対角線の長さをかけて2で割ったもの、つまり 『対角線×対角線÷2 ÷ 2 』 で求めることができます。 平行四辺形の一種でもあるので、底辺と高さが分かっていれば『底辺×高さ』でも求められます。 たとえば以下のような問題の場合。 例題 対角線がそれぞれ 6cm 6 c m 、 8cm 8 c m のひし形の面積を求めよ。 答えはこのよう 三角形が小さいときには平面三角形の底辺×高さ÷2になることを証明する道筋を紹介しよう。 まず, 余弦定理として本書p 66の(3 5)のほかにもう一つ補完的な定理がある。それは角と辺に関するもので次式である。
年 組 番 名前 5118 2 考え 2 台形の面積を求める公式を書いてみましょう。 台形の面積 = ( + )× ÷ 2 25 三角形が2つと考えました。 上底 下底 高さ点Pは毎秒2cmで動くので、底辺は $ 2x $ cmということになります。 底辺×高さ÷2にそのまま上の値と式を代入すると、 $ y=2x×6÷2=6x $ 次に $ x $ の変域ですが、Bの位置にいる時は $ x=0 $、Cまで8cmで点Pは毎秒2cmで動くので、8÷2=4‥4秒でCに着くことになります。 $ x $ の変域 $ 0≦x≦4 $ 次に $ y $ の変域ですが、$ x $ の変域 $ 0≦x≦4 $ の最大値「0」と最小値「4」を 上底辺 高さ 底辺 高さ 6×4÷2=12 9×4÷2=18 8×6÷2=24 55×8=44 7×6=42 12cm² (直線)AE 18cm² 24cm² 44cm² 42cm² 10cm² 3cm 2cm 4cm 4×2÷2=4 4×3÷2=6 4+6=10 右の四角形の面積を, 必要なところをはかって 求めましょう。 (式) 答え ( )



1




5年算数 台形の面積 指導実践 ネコ好きな学校の先生の日常
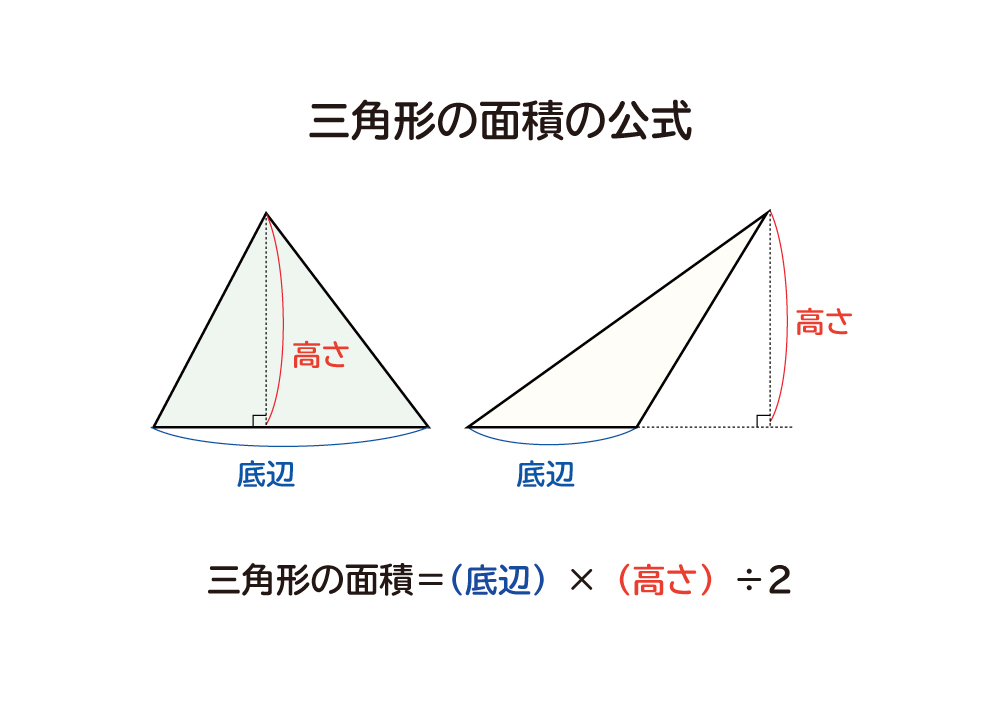
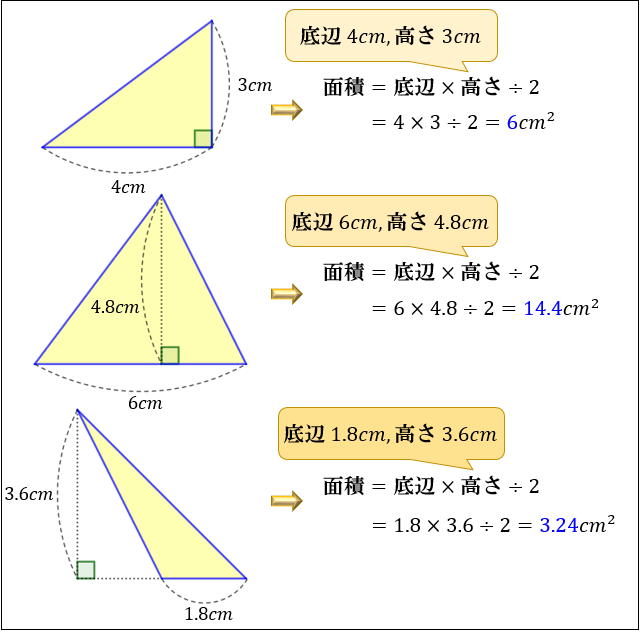
わかりますか? 高さ6cm 底辺8cm 復習2 式 三角形の面積の公 面積は 24㎠ 高さ6cm 式は 8×6÷2 底辺8cm 公式は 底辺 × 高さ ÷ 2 形のちがう三角形の面積 高さ 3㎝ 底辺4㎝ (1) 4×3÷2 =6㎠ 高さ 3㎝ 高さ 3㎝ 底辺4㎝ (2) 4×3÷2 =6㎠ 底辺4㎝ (3) 4×3÷2 =6㎠ 形がちがうのに、なんで、同じ面積になるのでしょうか? 底辺と高さの値が変わらないから 合体 いろんな形の 三角 底辺×高さ÷2ってのは 三角形の面積の式ですから直角三角形にこだわる必要はありませんよ 対角線を一本引いてみてください すると底辺をa、高さhの三角形と、底辺をb、高さhの三角形の二つに切ることができるでしょ 底辺aの三角形の面積はah/2 底辺bの三角形の面積はbh/2 二つのこうやって2つ重ねると、 平行四辺形を作ることができる んだよね! だから、三角形の面積を求めたければ 2つくっつけて 平行四辺形の面積を求める。 そして、 それを半分にする! という考え方を用いているのです。 平行四辺形の面積が (底辺)×(高



正三角形 辺から高さと面積 三角形の計算 計算サイト




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ
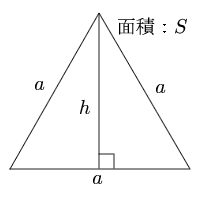
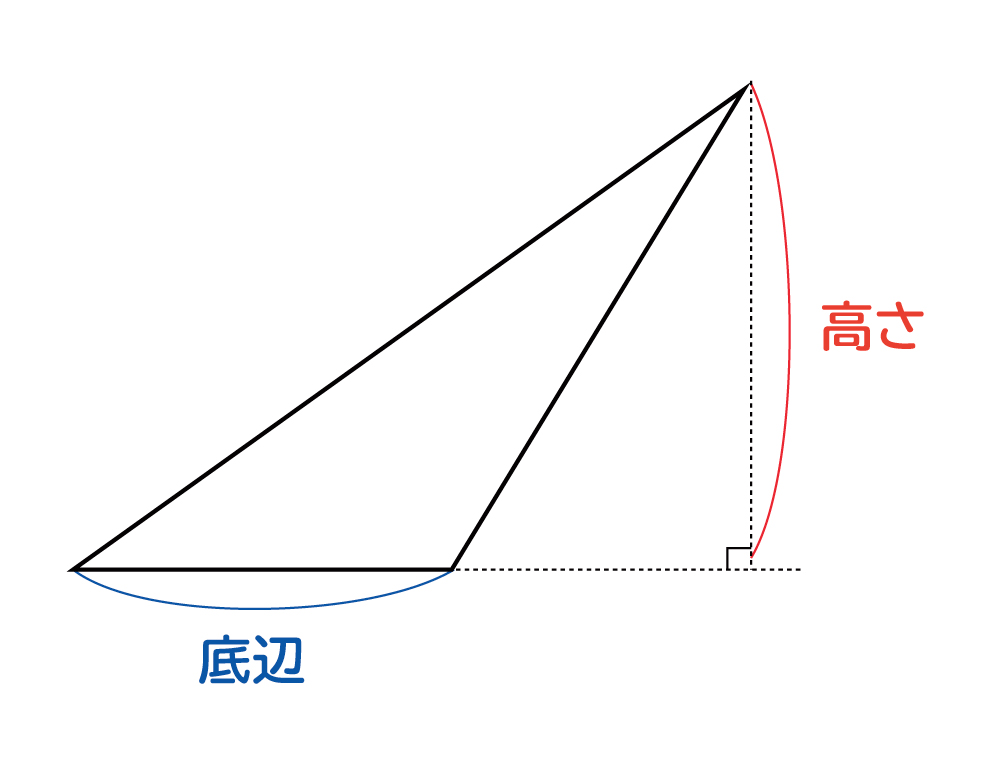
三角形の一辺の長さを『底辺』とし、頂点から底辺に向かって垂直に下ろした線の長さを『高さ』と言います。 このとき三角形の面積は『底辺×高さ ÷2 ÷ 2 』で求めることができます。 例題を見てみましょう。 例題 底辺 6cm 6 c m 、高さ 5cm 5 c m の三角形の面積を求めよ。 答えはこのように求めることができます。 6 ×5÷ 2=15(cm2) 6 × 5 ÷ 2 = 15 ( c m 2) 重要なのはということは、「底辺 × 高さ ÷2」は・・・=2年生の数学 三角形の 等積変形 とう せき へん けい 平成16年2月23日月曜日3校時 福嶺中学校コンピュータ室 山口 勇一
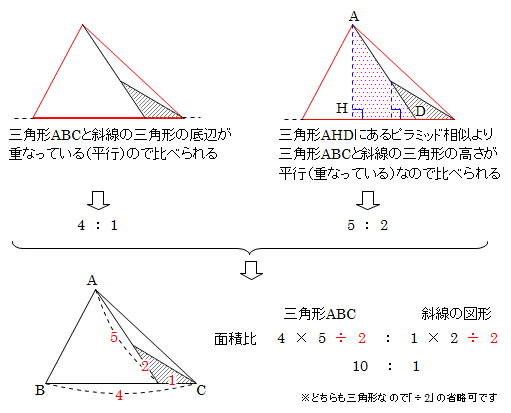



小5の学習ポイント4 辺の比と面積比 前田昌宏の中学受験が楽しくなる算数塾




Page 2 2 円の面積はなぜ 半径 半径 3 14 仕組み がわかれば算数は面白い ダ ヴィンチニュース
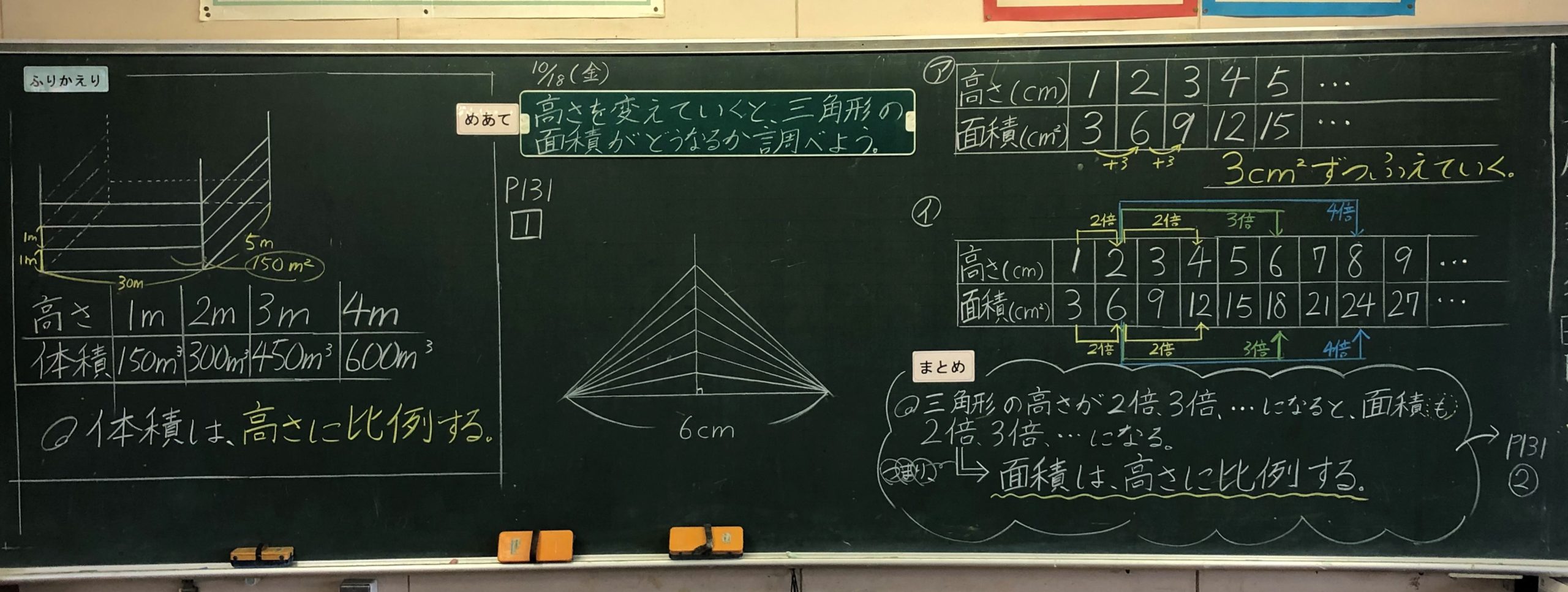
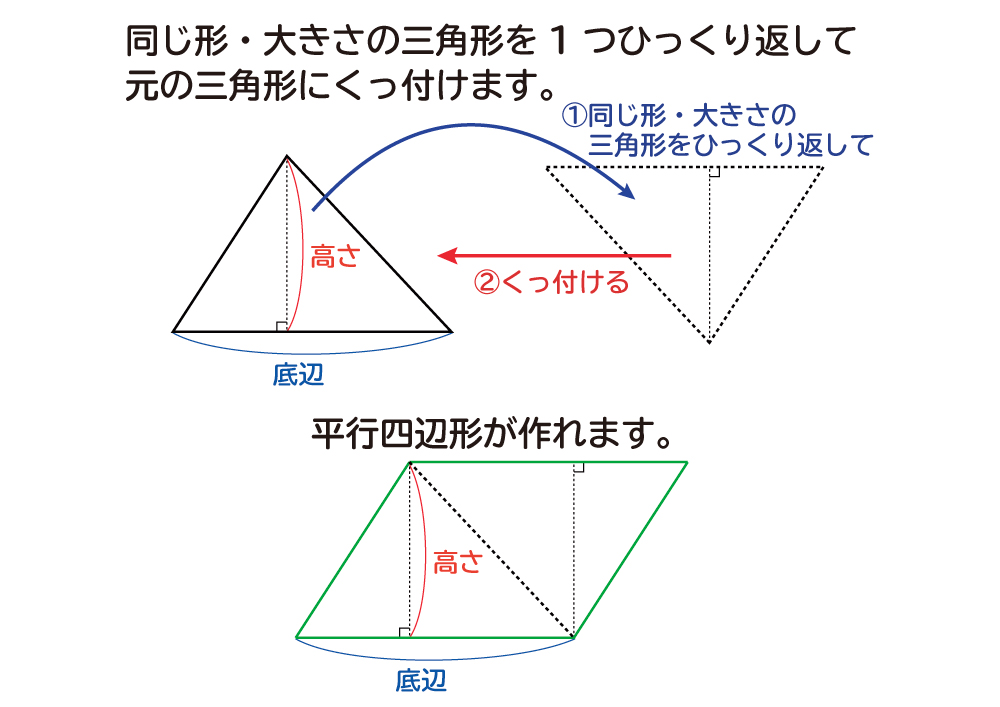
子ども 「底辺×高さ÷2!」 そのあと、いろんな三角形の底辺と高さを確かめたり、それをもとに平行四辺形の形がつくれたりするかどうかを確認します。 そうすれば、平行四辺形の半分の面積で求められることも、より印象づけられたのではと思います。台形の面積の公式を「よむ」5年生 右のように台形を 2つ組み合わせると平行四辺形ができます平行四辺 形の面積=底辺×高さで底辺のところが台形の上底+下底になってい ますだから台形の面積=(上底+下底)×高さ÷2です高さ (cm) 3 6 9 12 15 面積 (cm2) 9 18 27 36 45 〔三角形の高さと面積〕 比例する どの場合も, ÷ の答えが3になるので, 比例するといえます。 底辺を とすると cm 三角形の面積の公式は,「底辺×高さ÷2」なので, 高さ3,面積9を当てはめると,底辺の長さを




平行四辺形の面積の求め方 公式と計算例




台形の面積の公式 小学生に教えるための分かりやすい解説 数学fun
1/2 小学校6 年生 算数 面積 <三角形の面積> 高さ 底辺に垂直な直線ad 公式: 三角形の面積 = 底辺 × 高さ ÷ 2 問題:三角形の面積を求めましょう。 ① ② <平行四辺形の面積> 問題:平行四辺形の面積をまとめましょう。年 組 名前 取り組んだ日 月 日 = 底辺×高さ÷2 3日で飲んだ量を2 lとすると、1日 当たり何l飲んだことになりますか。底辺×高さ÷2 底辺×高さ÷2 サッカーおたくがアイドルにハマった話 と同じくらい音楽が好きで、ジャンル問わず何でも聴くし、音楽番組も見るし、同級生や職場の同僚に強火のエイターが居たので それが15年で、同じ年に関ジャムは始まっ
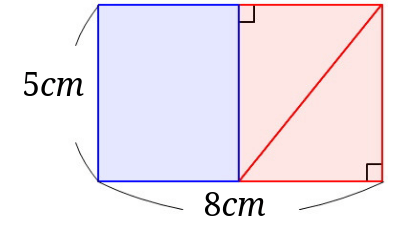



平行四辺形の面積の求め方で習う公式は なぜ底辺 高さになるの みけねこ小学校



面積の求め方は何年生で習いますか 正方形三角形平行四辺形は小学校4 5年で Yahoo 知恵袋
小学2年生の子にかさの単位変換を覚えてもらうにはどうしたら良いの? Wed 小学5年生で習う体積の意味は?かさと何が違うの? 三角形の面積はなぜ底辺×高さ÷2なの?鋭角三角形、直角三角形、鈍角三角形のそれぞれについて解説します!6年生 算数-4 修 三角形・四角形 唄は三角形,欝は平行四辺形,蔚は台形です。それぞれ面積は何或ですか。 唄欝蔚 唄 三角形の面積=底辺×高さ÷2より, 欝 平行四辺形の面積=底辺×高さより, 蔚 台形の面積=(上底+下底)×高さ÷2より, 練習問題 ↑図に底辺と高さを加えます。 子ども 「それから2でわると、24㎠になります。」 先生 「なるほど、じゃあ台形も、三角形と同じように底辺×高さ÷2で求められるね。」 板書します。




計算プリント Com Keisanprint تويتر
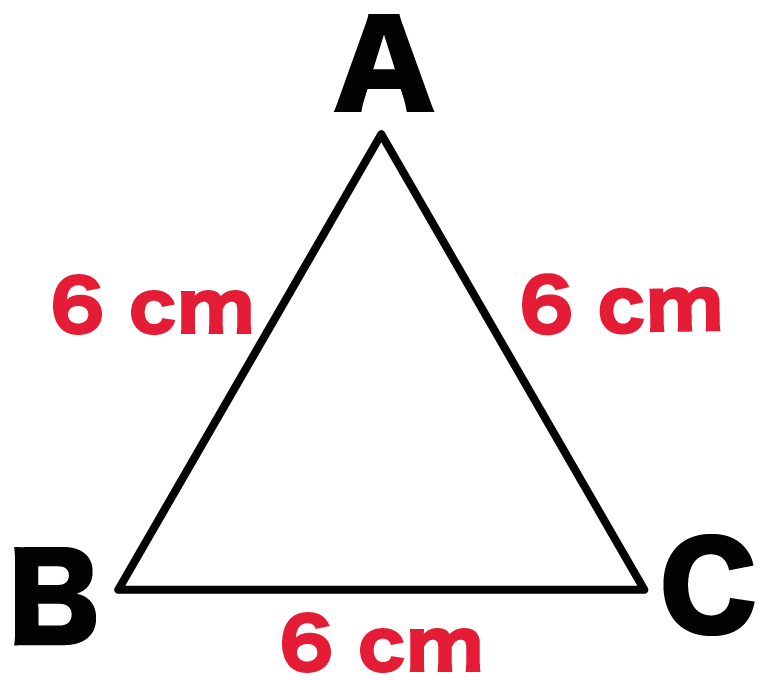



簡単公式 正三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
第3回図形問題を得意にするために意識したい学習の3つのステージ迫田 昂輝先生 こんにちは、迫田です。 今回からは、小学生のお子様が算数の学習に取り組む中で苦手に感じやすい単元や分野をピックアップして、それを得意に変えていくためのポイントをお伝えできればと考えて・ ひし形の面積の公式は, 対角線×対角線÷2 です。 三角形abcで,辺bcを底辺 ていへん とするとき,頂点aから底辺bcに垂直にひいた直 線の長さを高さといいます。 ・ 三角形の面積=底辺×高さ÷2 ・ 平行四辺形の面積=底辺×高さ解説 三角形の面積=底辺×高さ÷2 なので 10×2x÷2=10x y=10x 図2のように点Pが辺BC上にいるとき 図2 P 10cm 10cm 8cm xの変域を求めよ。 解説 AをスタートしてからBに到着するまで8÷2=4秒 AをスタートしてからCに到着するまで18÷2=9秒 よって点Pが辺BC上にいるのは4秒から




数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
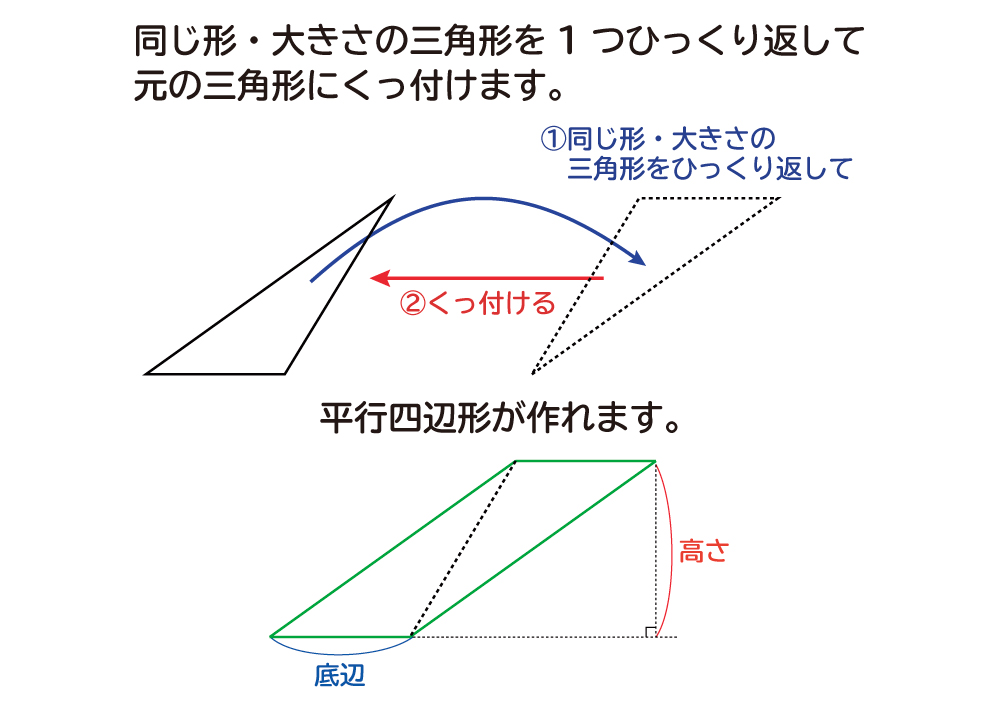



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル
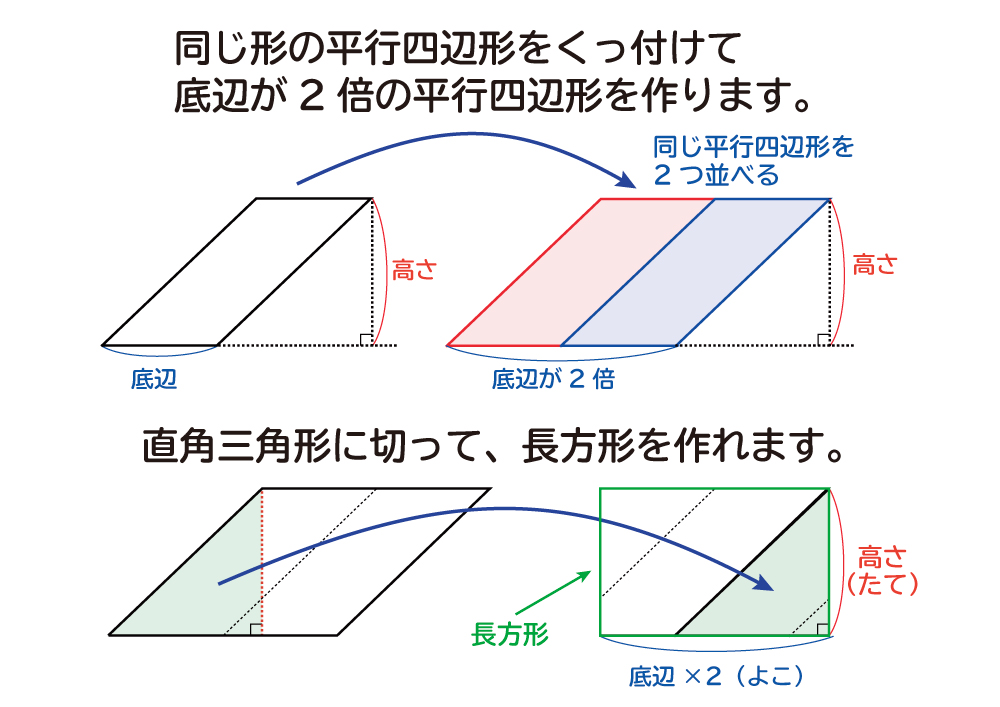
⑤ 台形 向かい合った1組の辺が平行な四角形 (上底+下底)×高さ÷2 ⑥ ひし形 すべての辺の長さが等しい四角形 対角線×対角線÷2 ※5年生では、上の表の①~⑥の三角形や四角形について、定義円周の長さを求める公式を覚えていますか。 ( 直径 )の長さ × ( 円周率 ) = 円周の長さ ですから、 直径が1cmのとき 1 × 314 = 314 答え 314cm 直径が2cmのとき 2 × 314 = 628 答え 628cm 直径が3cmのとき 3 × 314 = 942 答え 942cmです。 上の式や答えは、( 直径 )の長さで変わるだけですから、直径の長さを 、円周の長さ を〇で表すことにすると、上の式はすべて、T それで,平行四辺形の面積を求めるときのひみつは何ですか。 C 三角形の公式が底辺×高さ÷2だから,それが2枚あると言うことは,1つの三角形を2倍すればよいから,平行四辺形の面積は,底辺×高さになる。 C これでひみつが見つかった。
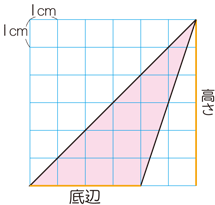



底辺と高さ 算数用語集
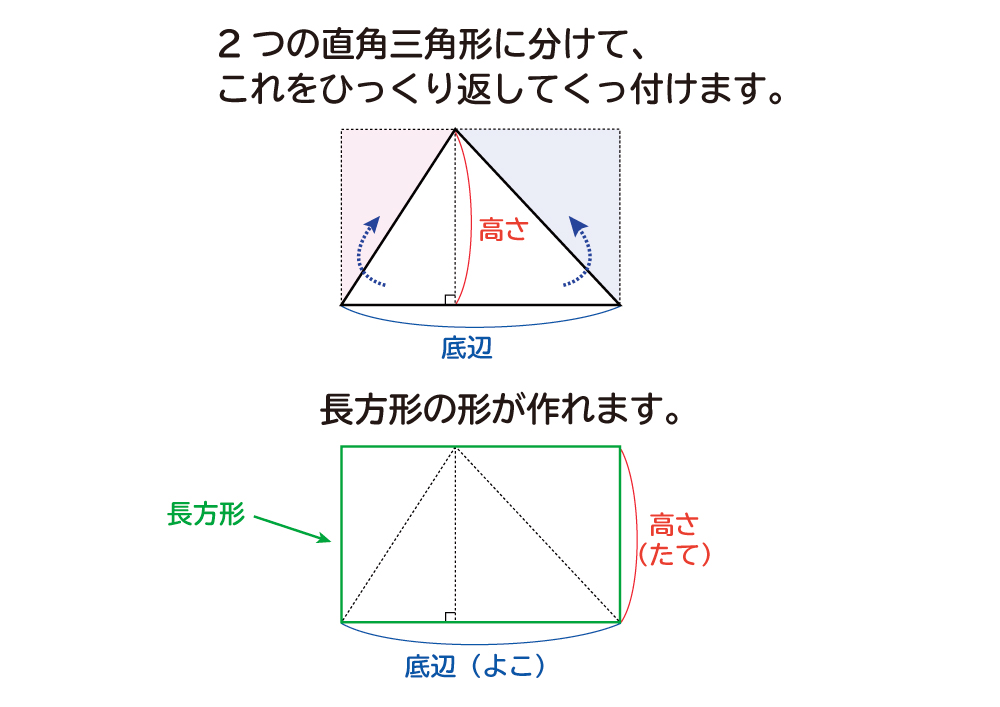



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル
カイト 面積の求め方は、底辺×高さ、で求められる。 カイト 三角形の面積の公式は底辺×高さ÷2だ。 カイト 同じ大きさの2つの三角形を組み合わせて四角形をつくる。 カイト そんで、その四角形の面積の半分が三角形1つの面積になるから、四角形の面積は「底辺×高さ」、その半分が三角形の面積だから「底辺×高さ÷2」となる。 ミズキ いいね。 それじゃ、今回に分ける。三角形ABFの面積を,底辺をAB, 高さをFHとして求めると, 6×8÷2=24(c㎡) となる。 三角形BEFの面積を,底辺をBE,高さを CFとして求めると, 3×4÷2=6(c㎡) となる。 したがって,四角形ABEFの面積は, 246=30 で,30c㎡である。 三角形の面積はなぜ底辺×高さ÷2で求められるの? 三角形は大きく分けて3種類あります。 直角三角形 1 3角形の角のうち1つが90°である三角形のことをいいます。 、鋭角三角形 2 三角形の3つの角、全てが90°より小さい三角形のことをいいます。 、鈍角三角形 3 三角形の角のうち1つの




この場合 ひなたさんがまるあになるのですが 説明のしかたが分かりません D Clear
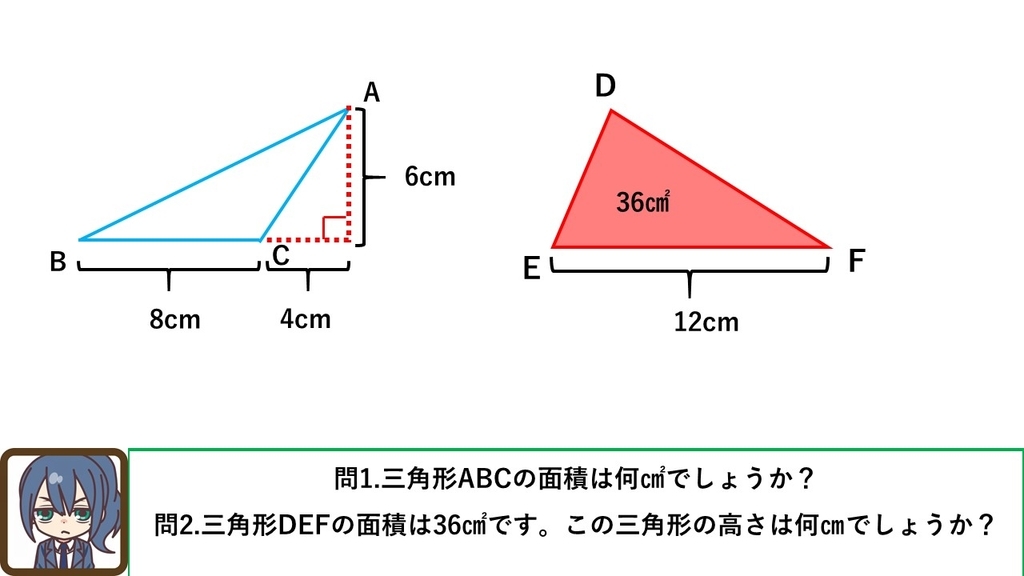



小学5年生 三角形の面積 答え Active Learning 学院
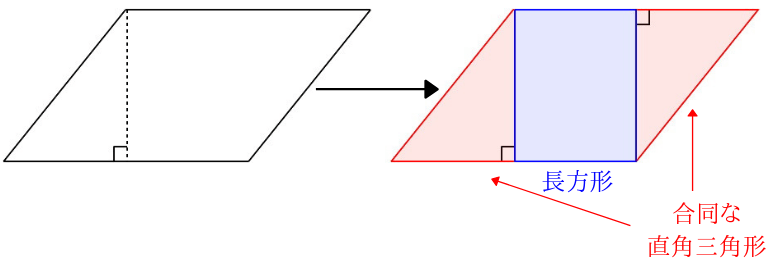
「底辺 × 高さ ÷ 2」の公式に数字をあてはめるわけですが、この方法で高さを探すと30°二等辺三角形では次のようなことに気づくと思います。 底辺=斜辺; 2 「ひし形」「タコ形」 「二つの対角線をかけて2で割る」 で求められますが、延長して長方形を作って求めるという理屈も押さえておきましょう。 また、「ひし形」は 平行四辺形の一種でもありますので、「底辺」×「高さ」でも求められること も忘れないようにしておきましょう。



三角形と台形の面積
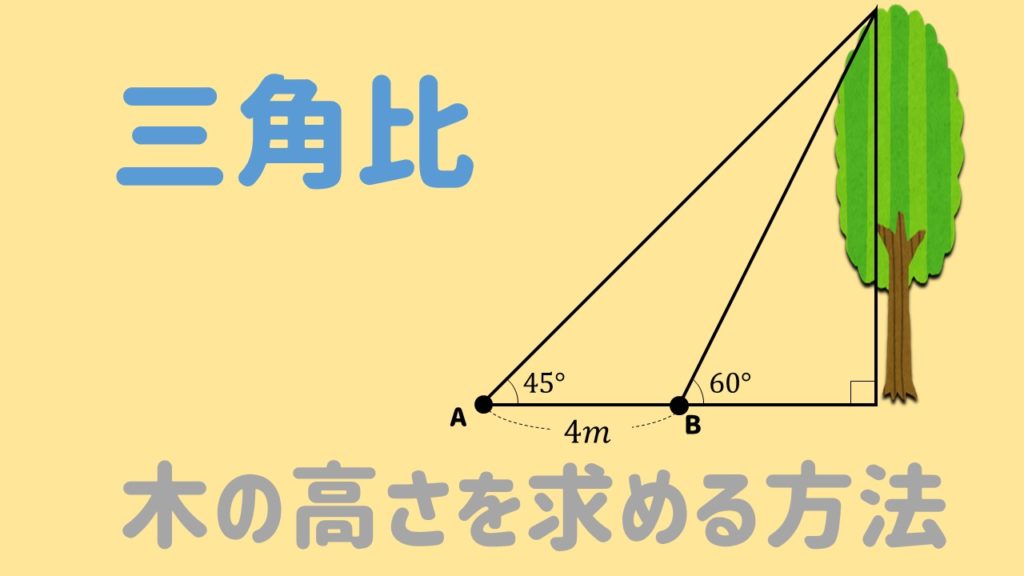



高1数学 木の高さを三角比を用いて求める方法を解説 数スタ




平行四辺形の面積の求め方 公式と計算例




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
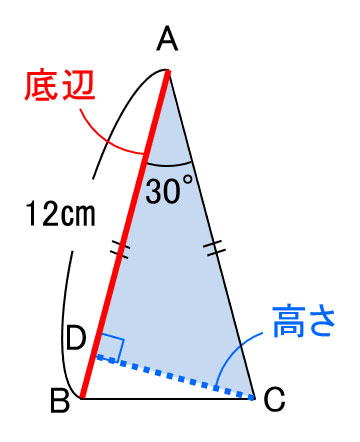



中学受験算数のちょ 怪しい三角形 中学受験プロ講師ブログ




簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
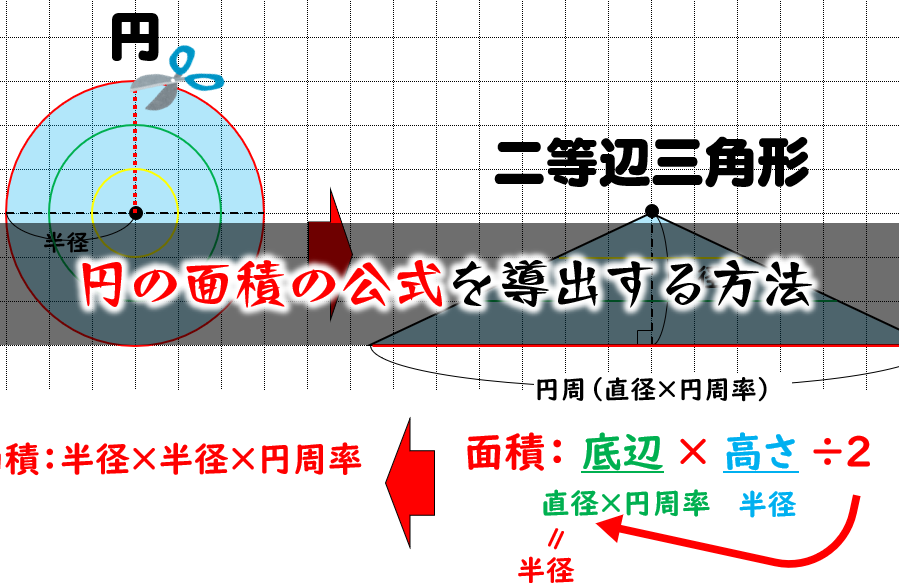



円の面積の公式 なぜ半径と円周率で求められるのか を小学生に分かりやすく説明する方法 数学fun




直角三角形の辺の長さ 合同条件 面積について アタリマエ



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル



三角形の面積公式 小学生はどうやって解く 問題を使って解説 数スタ




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




三角形の面積の公式 2 って どうして2で割るの



5年生算数 面積 黒板log 黒板log
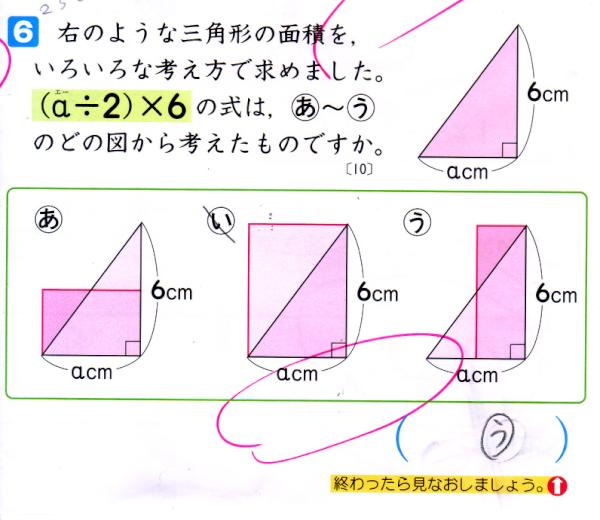



堀内 真 A Twitter 5年生のときに 三角形の面積は 底辺 高さ 2 と立式しないと 答えは合っているけど式が間違い と教えられた子どもが 6年生では 底辺 2 高さ でもいいと教えられる ちなみに この を省略するとバツになるのだろうか 青葉出版6年




三角形の面積の求め方とは Sinやベクトルを用いる公式も解説 小学生から高校生まで 遊ぶ数学
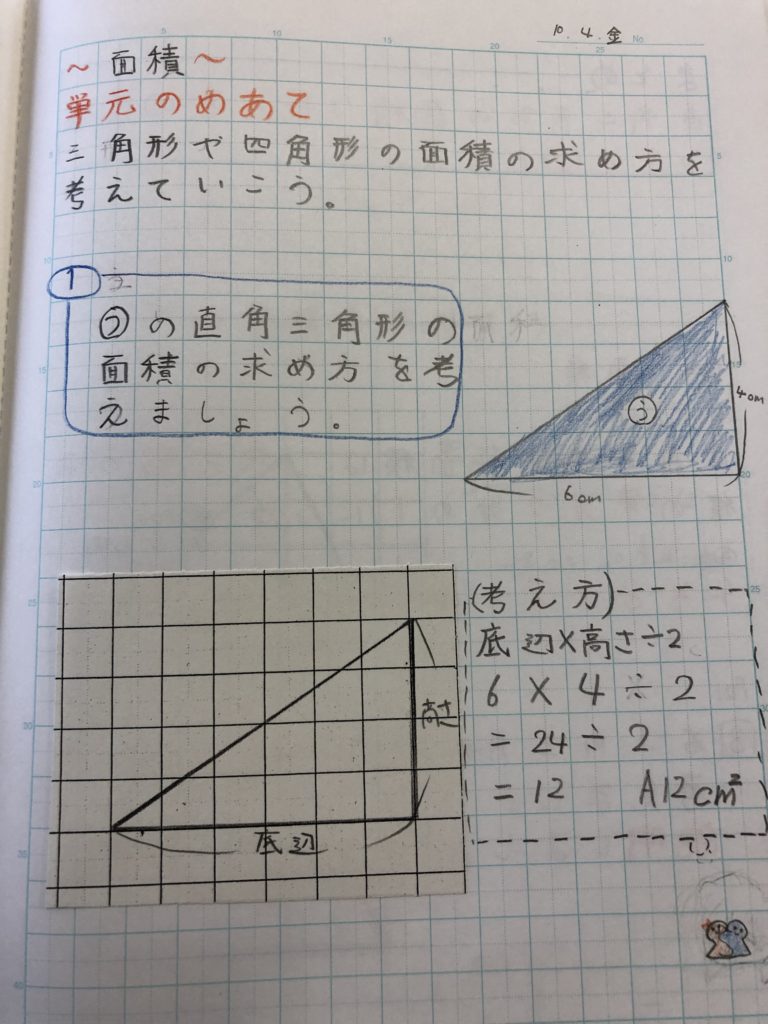



5年生算数 面積 黒板log 黒板log




小学生の算数センス 256が 解ける子 と 解けない子 の差 Sankeibiz サンケイビズ
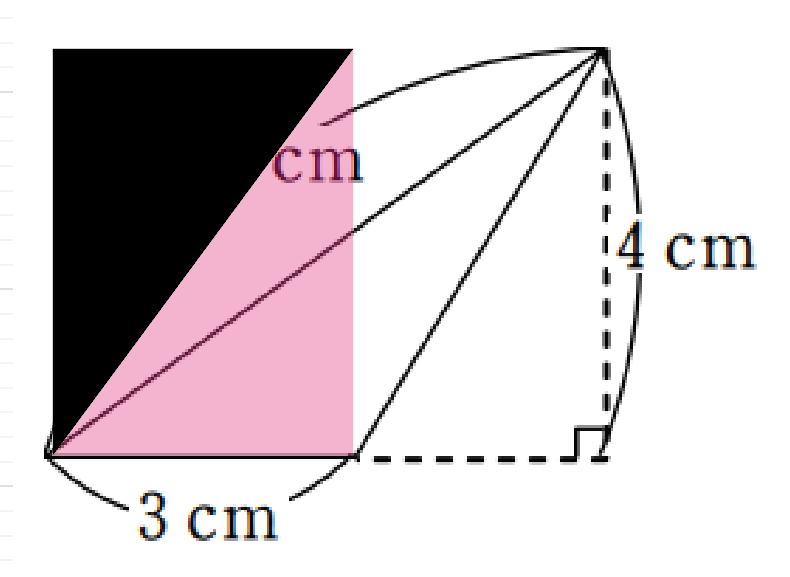



小学校5年生の算数 三角形の面積計算 をやってみた 赤髪デザイナーmoekoosawaカラフルdays
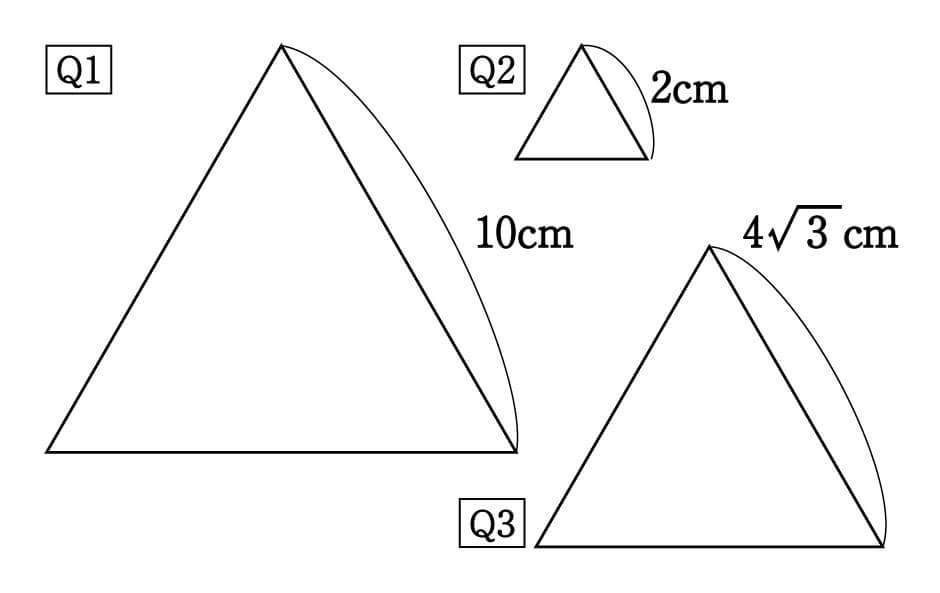



数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




台形の任意の高さにおける上辺の長さ 相似関係の2つの台形の高さがそれぞれ Okwave




底辺 Wikipedia




マスラボ 小学5年生 三角形の面積 高さや底辺を求める Youtube




台形の面積の求め方 公式と計算例




小学校5年生の算数 三角形の面積計算 をやってみた 赤髪デザイナーmoekoosawaカラフルdays



画像の三角形abcの面積は何平方センチメートルですか 辺abを底 Yahoo 知恵袋
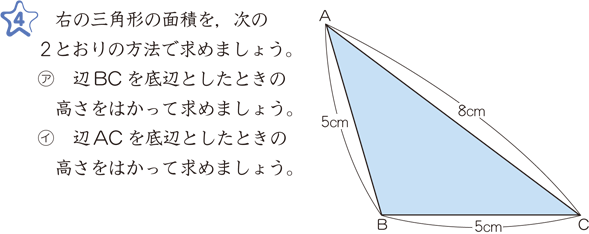



底辺と高さ 算数用語集




掛け算の順序をめぐって 公式とかけ算の順序




平面図形の苦手を解消 三角形の面積比 基本編




すきるまドリル 小学5年生 算数 図形の面積 無料学習プリント すきるまドリル 無料学習プリント




至急 この下の写真の問題の がわかりません Clear




小5 算数 小5 42 三角形の面積 Youtube



記事 詳細情報 19年 12月 11日 水曜日 5年 算数 平行四辺形の面積 平行四辺形の面積の求め方は 底辺 高さ う ん 高さはどれだ 5年生の算数は 新しいことが盛りだくさんです 何年生の算数も大事だけど 6年 中学の元になるような




面積 平行四辺形の面積 01 高さが外にあるときの面積の求め方 Youtube




三角形の面積を求める公式7選 高校数学のまとめにどうぞ



3



3



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル




四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル



底辺 高さ 2は小学何年で習いますか Yahoo 知恵袋



平行四辺形の面積の求め方で習う公式は なぜ底辺 高さになるの みけねこ小学校



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
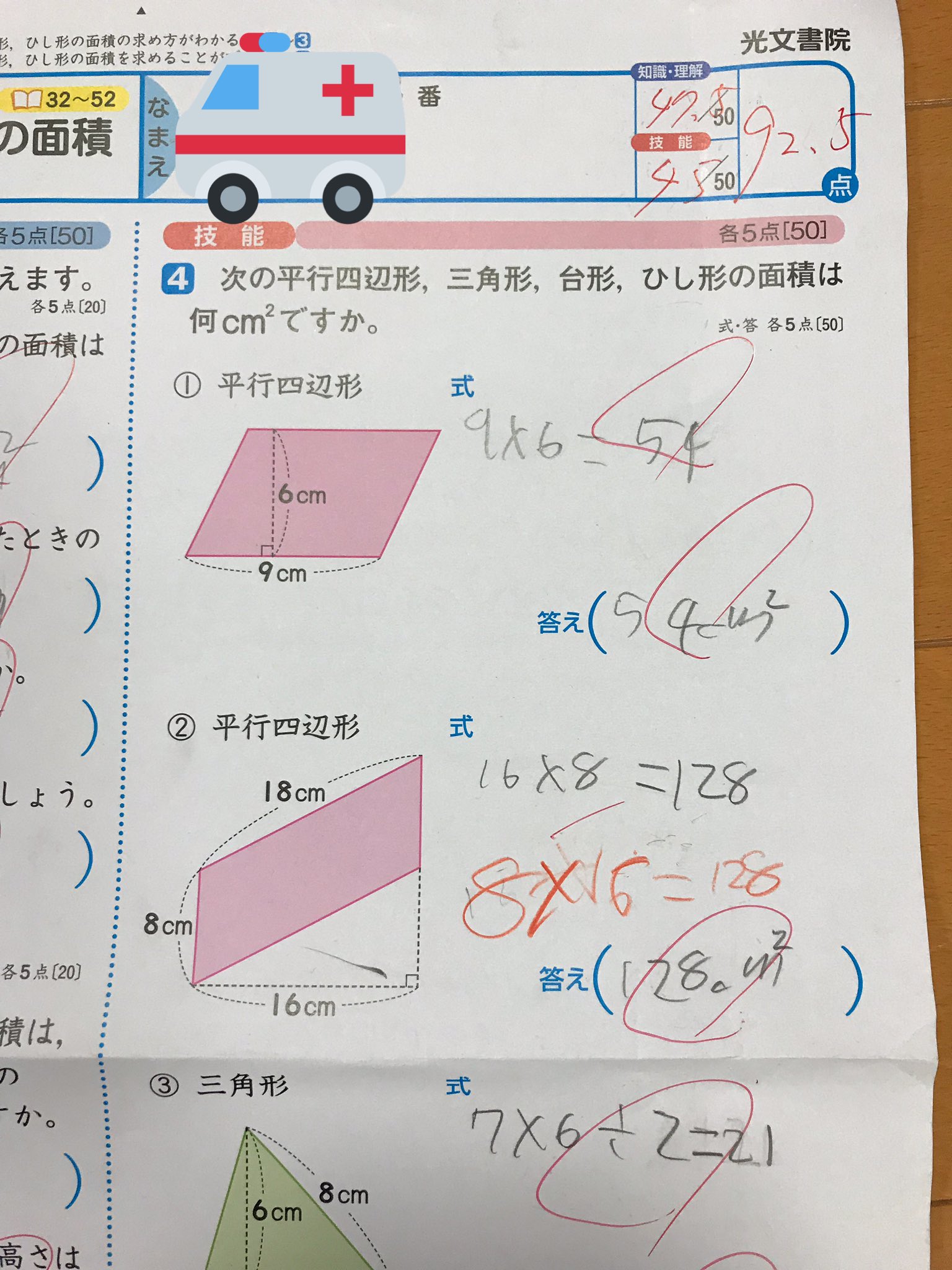



ストさん 5年生の息子の算数のテスト 平行四辺形の面積の公式は底辺 高さであり 高さ 底辺ではないから 答えは正解だけど 式は不正解でマイナス5点だと 小学校の先生は馬鹿なのか 信じられない
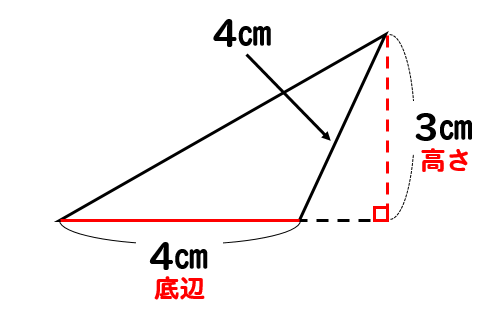



三角形の面積公式 小学生はどうやって解く 問題を使って解説 数スタ




小学5年生 三角形の面積 算数 Active Learning 学院



Http Www Nkc City Narashino Chiba Jp Nkc Gakusyu P San 6 Mojisiki2 Pdf




これまでで最高の三角形 の 底辺 子供のための最高のぬりえ




三角形の面積公式 小学生はどうやって解く 問題を使って解説 数スタ




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
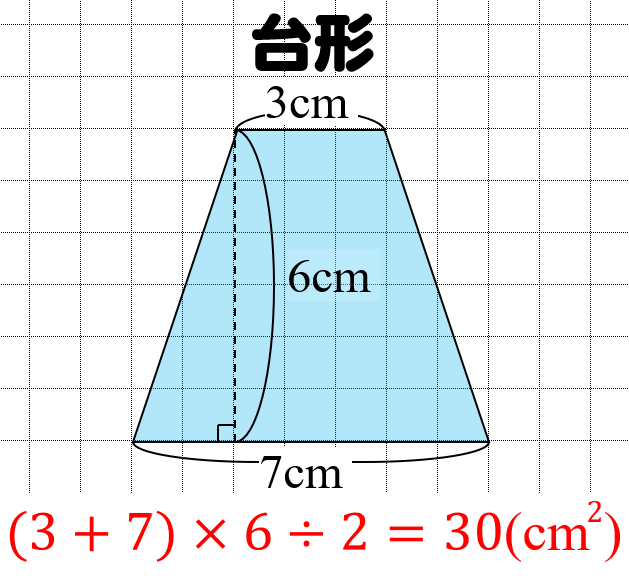



台形の面積の公式 小学生に教えるための分かりやすい解説 数学fun
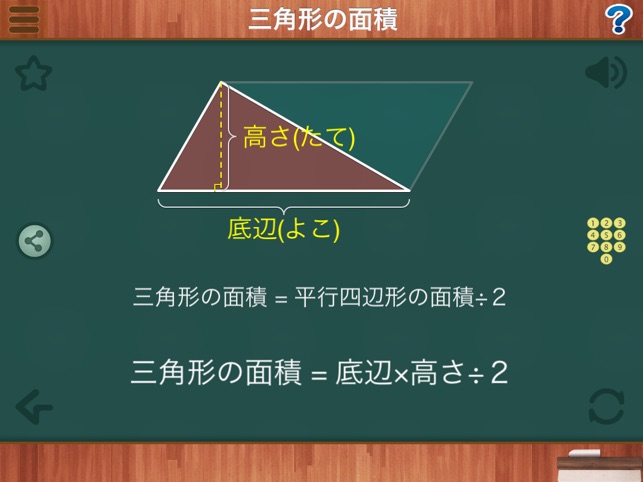



小学算数アニメーション 1 6年生 をapp Storeで




平行四辺形の面積は 底辺 高さ かけ算の順序の昔話




面積の求め方 計算公式一覧




簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
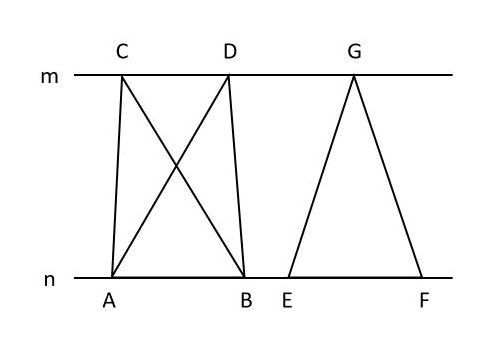



等積変形で難しい面積問題をサクッと解決 平行線と三角形の関係がおもしろい 中学受験ナビ
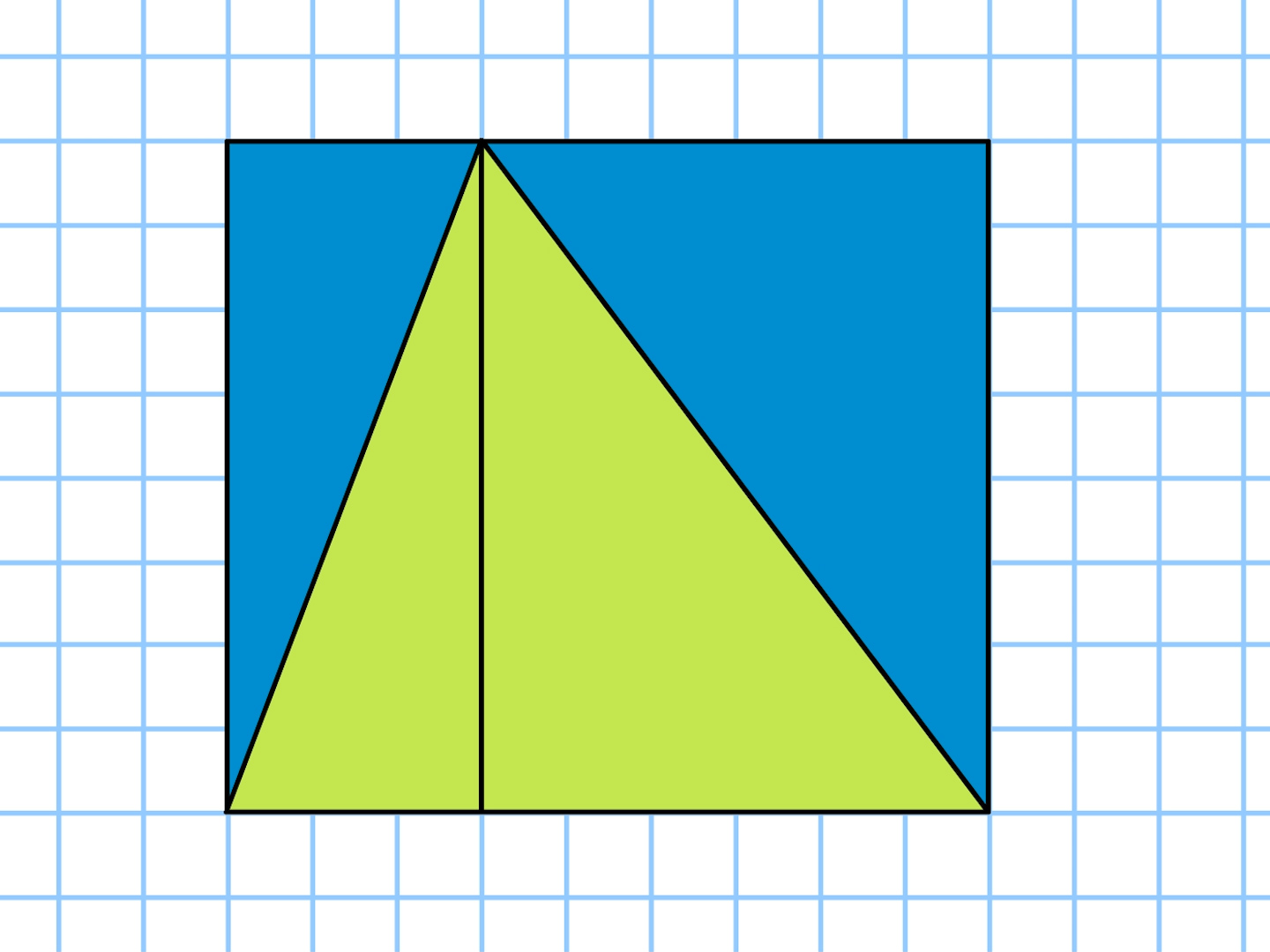



5年 三角形の面積 算数イメージ動画集 大日本図書
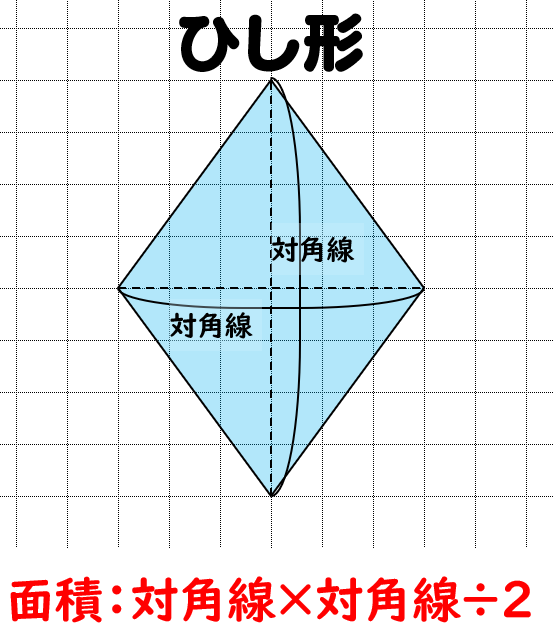



ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun




面積の求め方 計算公式一覧
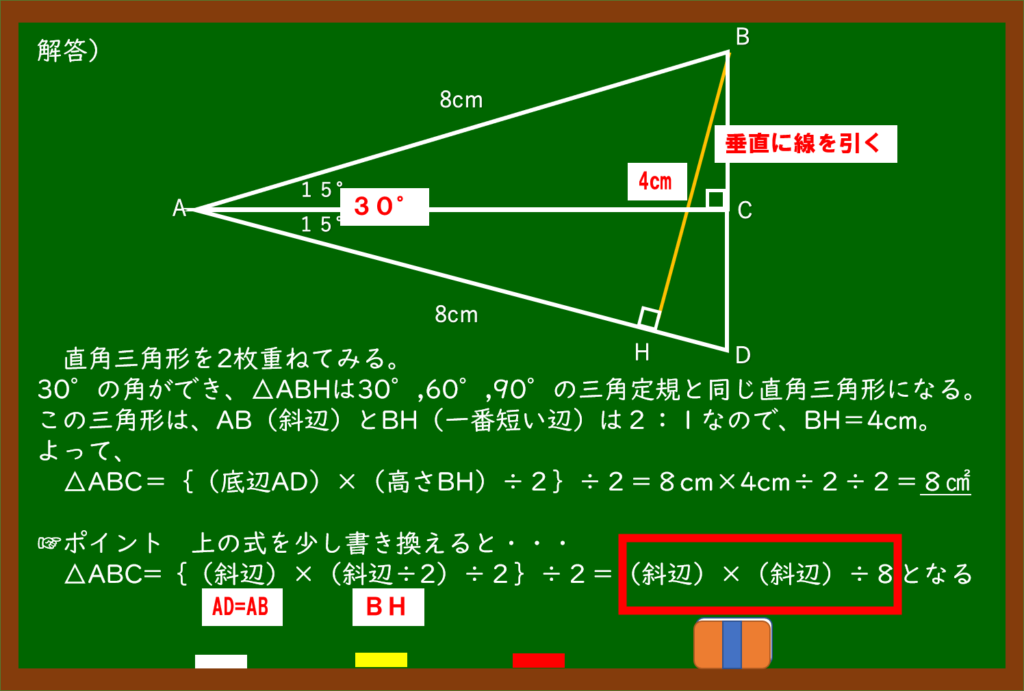



たのしい算数 入試問題にチャレンジ 面積の問題だけど キッズライト 公式サイト 福岡 西都小学校前の学童保育 学習塾 四谷大塚net 東進こども英語塾



これまでで最高の三角形 の 底辺 子供のための最高のぬりえ




小学6年生で三角形の面積求め方わかりません 小学6年生の親です 学 数学 教えて Goo



小学校5年生の算数 三角形の面積計算 をやってみた 赤髪デザイナーmoekoosawaカラフルdays




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun



底辺 高さ 2は小学何年で習いますか Yahoo 知恵袋



なぜ 平行四辺形の面積は 底辺 高さ なのか を説明します おかわりドリル
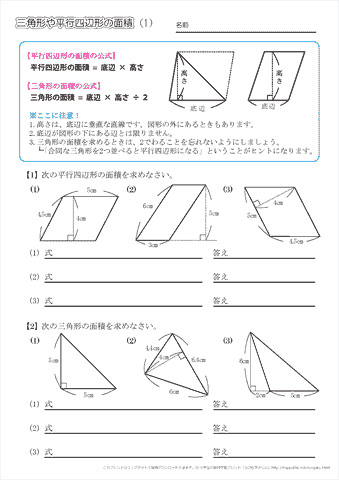



小学5年生の算数 三角形や平行四辺形の面積 問題プリント ちびむすドリル 小学生
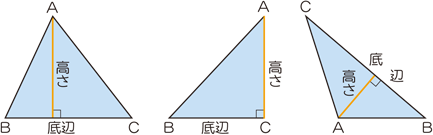



底辺と高さ 算数用語集




21年2月19日 金 算数の特訓 とろんこアカデミー



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生



しょうちゃん 公式ブログ 算数の問題を解いてみる その15 図形 円の面積 Powered By Line
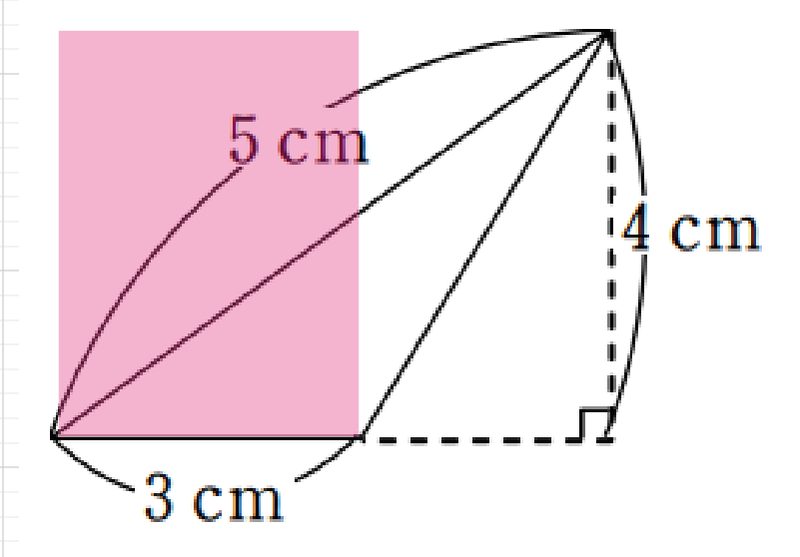



小学校5年生の算数 三角形の面積計算 をやってみた 赤髪デザイナーmoekoosawaカラフルdays




三角形の面積の求め方とは Sinやベクトルを用いる公式も解説 小学生から高校生まで 遊ぶ数学



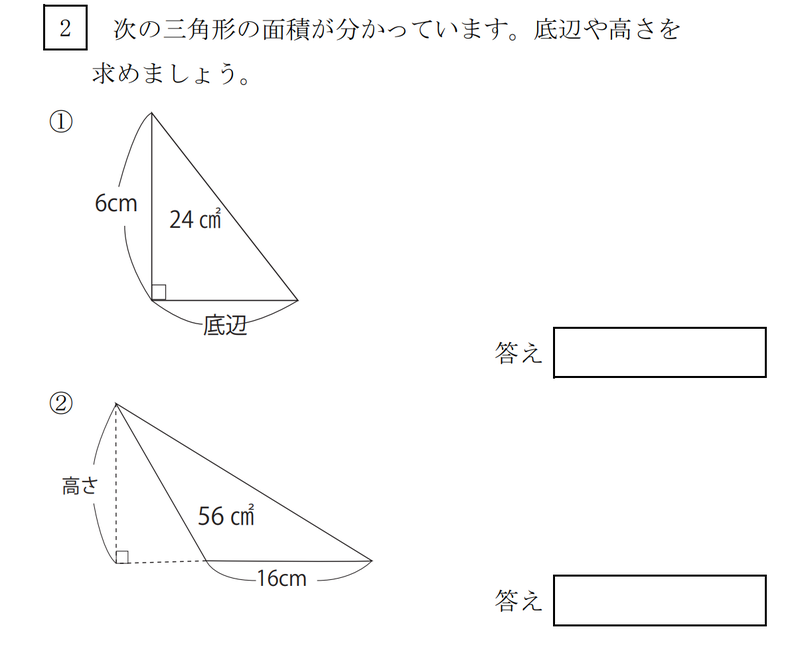
小学校5年生の宿題なのですが面積を求めてからの高さ X の求め方の公式を教え Yahoo 知恵袋



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生
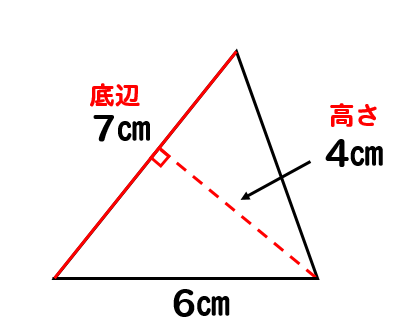



三角形の面積公式 小学生はどうやって解く 問題を使って解説 数スタ



Kids Gakken Co Jp Box Sansu 05 Pdf B Pdf
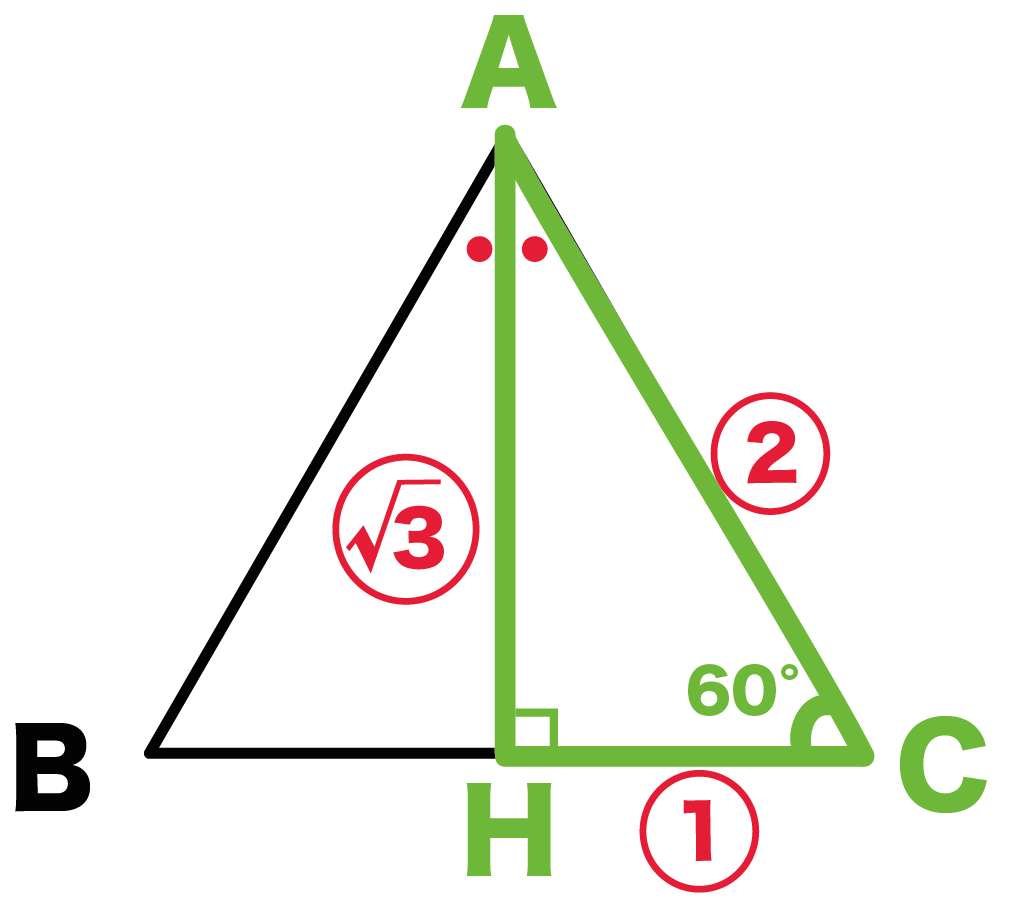



簡単公式 正三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




平面図形の苦手を解消 三角形の面積比 基本編




小5算数 三角形の面積 高さを求める Youtube




ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun
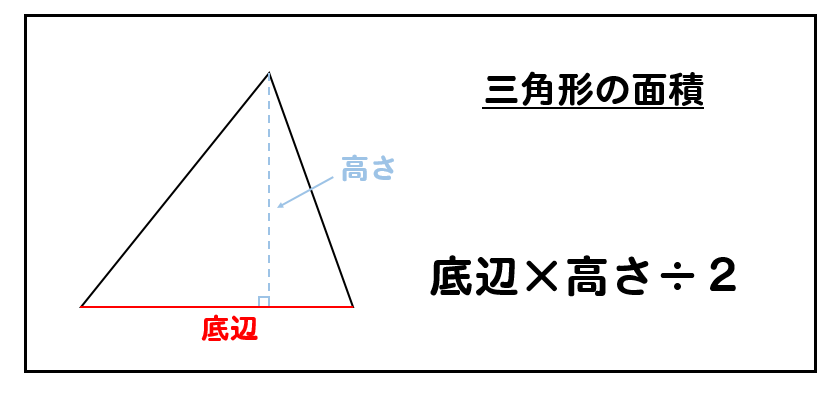



三角形の面積公式 小学生はどうやって解く 問題を使って解説 数スタ




小学5年生 ひし形 台形の面積 算数 Active Learning 学院



3




小学校5年生の算数 三角形の面積計算 をやってみた 赤髪デザイナーmoekoosawaカラフルdays



三角形と台形の面積



0 件のコメント:
コメントを投稿